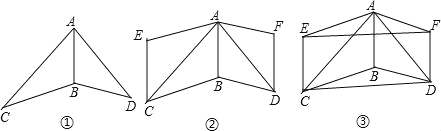
【题目】在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.
小明做了如下操作:
将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:
(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;
(2)连接EF,CD,如图③,求证:四边形CDFE是平行四边形.
参考答案:
【答案】(1)四边形ABDF是菱形.理由见解析;(2)证明见解析.
【解析】
试题分析:(1)根旋转的性质得AB=DF,BD=FA,由于AB=BD,所以AB=BD=DF=FA,则可根据菱形的判定方法得到四边形ABDF是菱形;
(2)由于四边形ABDF是菱形,则AB∥DF,且AB=DF,再根据旋转的性质易得四边形ABCE为平行四边形,根据平行四边形的性质得AB∥CE,且AB=CE,所以CE∥FD,CE=FD,所以可判断四边形CDEF是平行四边形.
试题解析:(1)四边形ABDF是菱形.理由如下:
∵△ABD绕着边AD的中点旋转180°得到△DFA,
∴AB=DF,BD=FA,
∵AB=BD,
∴AB=BD=DF=FA,
∴四边形ABDF是菱形;
(2)∵四边形ABDF是菱形,
∴AB∥DF,且AB=DF,
∵△ABC绕着边AC的中点旋转180°得到△CEA,
∴AB=CE,BC=EA,
∴四边形ABCE为平行四边形,
∴AB∥CE,且AB=CE,
∴CE∥FD,CE=FD,
∴四边形CDEF是平行四边形.
-
科目: 来源: 题型:
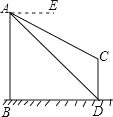
查看答案和解析>>【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是()
A. 10π B. 15π C. 20π D. 25π
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x1,x2是一元二次方程x2-2x-5=0的两根,则x12+x22的值为( )
A. 6 B. 8 C. 14 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三内角的度数的比为1:1:2,则此三角形( )
A.锐角三角形
B.钝角三角形
C.等边三角形
D.等腰直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】若梯形的中位线长为8,高为4,则梯形的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A. ∠D=90° B. AB=CD
C. AD=BC D. BC=CD
相关试题

