【题目】圆锥的底面周长为6πcm,高为4cm,则该圆锥的全面积是;侧面展开扇形的圆心角是 .
参考答案:
【答案】24π;216°
【解析】解:设圆锥的底面半径为r,母线长为R,侧面展开扇形的圆心角为n°; ∵圆锥的底面周长为2πr=6πcm,
∴r=3,
∵圆锥的高为4cm,
∴R= ![]() =5(cm),
=5(cm),
∴圆锥的全面积=底面积+侧面积=π×32+ ![]() ×6π×5=24π,
×6π×5=24π,
∵侧面展开扇形的弧长l=底面周长=6π= ![]() ,
,
∴n= ![]() =216,
=216,
即侧面展开扇形的圆心角是216°;
所以答案是:24π,216°.
【考点精析】本题主要考查了圆锥的相关计算的相关知识点,需要掌握圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,(1)∠AOC是哪两个角的和;(2)∠AOB是哪两个角的差;
(3)如果∠AOB=∠COD,那么∠AOC与∠DOB相等吗?
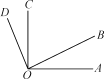
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中,其正确命题的个数是( ) ①若a>b,则
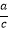 >
> 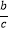 ;②垂直于弦的直径平分弦;③平行四边形的对角线互相平分;④反比例函数y=
;②垂直于弦的直径平分弦;③平行四边形的对角线互相平分;④反比例函数y= 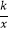 ,当k<0时,y随x的增大而增大.
,当k<0时,y随x的增大而增大.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
 是等腰直角三角形,
是等腰直角三角形, ,点D是BC的中点
,点D是BC的中点 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG. 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______; 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转 ,
, 判断
判断 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论; 若
若 ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题背景:
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;

(2)探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=
 ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;(3)结论应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角∠EOF=70°,试求此时两舰艇之间的距离.
(4)能力提高:
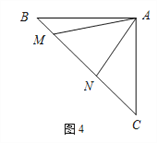
如图4,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,试求出MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰
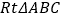 中,
中,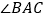 =90°,
=90°,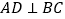 于
于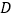 ,
,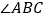 的平分线分别交
的平分线分别交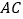 、
、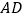 于
于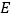 、
、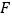 两点,
两点,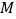 为
为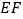 的中点,延长
的中点,延长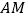 交
交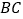 于点
于点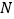 ,连接
,连接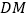 .下列结论:①
.下列结论:① 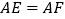 ;②
;② 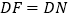 ;③
;③ 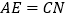 ;④
;④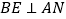 ;上述结论中正确的个数是( )
;上述结论中正确的个数是( )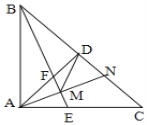
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
相关试题

