搜索
【题目】（1）计算：
（2）先化简，再求代数式的值：
，其中a=（﹣1）2014+tan60°．
参考答案：
【答案】（1）
；（2）化简结果：
，值：
．
【解析】
试题分析：（1）分别根据负整数指数幂的计算法则、特殊角的三角函数值及绝对值的性质分别计算出各数，再根据实数混合运算的法则进行计算即可；（2）先根据实数混合运算的法则把原式进行化简，再求出a的值代入进行计算即可．
试题解析：（1）根据负整数指数幂的计算法则、特殊角的三角函数值及绝对值的性质分别计算出各数，再根据实数混合运算的法则进行计算:原式=﹣
+|1﹣
|（2+2
）=﹣
+|1﹣|×2（1+）=﹣
+2（﹣1）（+1）=﹣+2=
；（2）先根据实数混合运算的法则把原式进行化简，原式=
=，再求出a的值，∵a=1+，∴原式=
=．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中：①角平分线上的点到角两边距离相等；②等腰三角形至少有1条对称轴，至多有3条对称轴；③等腰梯形对角线相等；④全等的两个图形一定成轴对称.其中正确有（ ）
A. 4个 B. 3个 C. 2个 D. 1个
-
科目： 来源： 题型：
查看答案和解析>>【题目】请写出一个大于8而小于10的无理数： ．
-
科目： 来源： 题型：
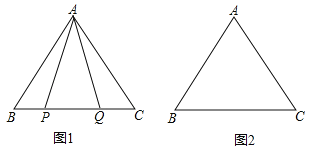
查看答案和解析>>【题目】在等边△ABC中：
（1）如图1，P，Q是BC边上的两点，AP=AQ，∠BAP=20°，求∠AQB的度数；
（2）点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC的对称点为M，连接AM，PM．
①依题意将图2补全；
②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：要证明PA=PM，只需证△APM是等边三角形；
想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；
想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…
请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个有理数的平方根和立方根相同，那么这个数是（ ）
A.±1
B.0
C.1
D.0和1 -
科目： 来源： 题型：
查看答案和解析>>【题目】下列等式中，不一定成立的是（ ）
A.3m2﹣2m2＝m2B.m2m3＝m5C.（m+1）2＝m2+1D.（m2）3＝m6
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况，随机抽样调查了某校初一学生一个学期参加综合实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图（如图）．
请你根据图中提供的信息，回答下列问题：
（1）求出扇形统计图中
的值，并求出该校初一学生总数；（2）分别求出活动时间为5天、7天的学生人数，并补全频数分布直方图；
（3）求出扇形统计图中“活动时间为4天”的扇形所对圆心角的度数；
（4）在这次抽样调查中，众数和中位数分别是多少？
（5）如果该市共有初一学生6000人，请你估计“活动时间不少于4天”的大约有多少人？
相关试题
