【题目】已知边长为4的正方形ABCD,顶点A与坐标原点重合,一反比例函数图象过顶点C,动点P以每秒1个单位速度从点A出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC﹣CB﹣BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
(1)求出该反比例函数解析式;
(2)连接PD,当以点Q和正方形的某两个顶点组成的三角形和△PAD全等时,求点Q的坐标;
(3)用含t的代数式表示以点Q、P、D为顶点的三角形的面积s,并指出相应t的取值.

参考答案:
【答案】(1)y=![]() ;
;
(2)Q1(![]() ,4);Q2(4,
,4);Q2(4,![]() ),Q3(4,
),Q3(4,![]() );
);
(3)s1=8t(0<t≤1);s2=﹣2t2+2t+8(1≤t≤2);s3=﹣10t+24(2≤t≤![]() ).
).
【解析】
试题(1)根据正方形ABCD的边长为4,可得C的坐标为(4,4),再用待定系数法求出反比例函数解析式;
(2)分点Q在CD,BC,AB边上,根据全等三角形的判定和性质求得点Q的坐标;
(3)分点Q在CD,BC,AB边上,由三角形面积公式和组合图形的面积计算即可求解.
试题解析:解:(1)∵正方形ABCD的边长为4,
∴C的坐标为(4,4),
设反比例解析式为y=![]() ,
,
将C的坐标代入解析式得:k=16,则反比例解析式为y=![]() ;
;
(2)当Q在DC上时,如图所示:
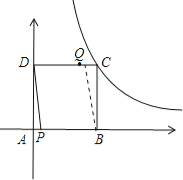
此时△APD≌△CQB,
∴AP=CQ,即t=4﹣4t,解得t=![]() ,
,
则DQ=4t=![]() ,即Q1(
,即Q1(![]() ,4);
,4);
当Q在BC边上时,有两个位置,如图所示:
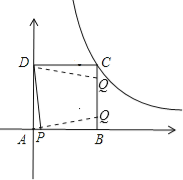
若Q在上边,则△QCD≌△PAD,
∴AP=QC,即4t﹣4=t,解得t=![]() ,
,
则QB=8﹣4t=![]() ,此时Q2(4,
,此时Q2(4,![]() );
);
若Q在下边,则△APD≌△BQA,
则AP=BQ,即8﹣4t=t,解得t=![]() ,
,
则QB=![]() ,即Q3(4,
,即Q3(4,![]() );
);
当Q在AB边上时,如图所示:
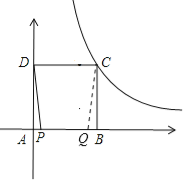
此时△APD≌△QBC,
∴AP=BQ,即4t﹣8=t,解得t=![]() ,
,
因为0≤t≤![]() ,所以舍去.
,所以舍去.
综上所述Q1(![]() ,4); Q2(4,
,4); Q2(4,![]() ),Q3(4,
),Q3(4,![]() );
);
(3)当0<t≤1时,Q在DC上,DQ=4t,则s=![]() ×4t×4=8t;
×4t×4=8t;
当1≤t≤2时,Q在BC上,则BP=4﹣t,CQ=4t﹣4,AP=t,
则s=S正方形ABCD﹣S△APD﹣S△BPQ﹣S△CDQ=16﹣![]() APAD﹣
APAD﹣![]() PBBQ﹣
PBBQ﹣![]() DCCQ=16﹣
DCCQ=16﹣![]() t×4﹣
t×4﹣![]() (4﹣t)[4﹣(4t﹣4)]﹣
(4﹣t)[4﹣(4t﹣4)]﹣![]() ×4(4t﹣4)═﹣2t2+2t+8;
×4(4t﹣4)═﹣2t2+2t+8;
当2≤t≤![]() 时,Q在AB上,PQ=12﹣5t,则s=
时,Q在AB上,PQ=12﹣5t,则s=![]() ×4×(12﹣5t),即s=﹣10t+24.
×4×(12﹣5t),即s=﹣10t+24.
总之,s1=8t(0<t≤1);
s2=﹣2t2+2t+8(1≤t≤2);
s3=﹣10t+24(2≤t≤![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
 ,
, 给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,
给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1, ),(2,
),(2, ),都是“同心有理数对”.
),都是“同心有理数对”.(1)数对(﹣2,1),(3,
 )是 “同心有理数对”的是__________.
)是 “同心有理数对”的是__________.(2)若(a,3)是“同心有理数对”,求a的值;
(3)若(m,n)是“同心有理数对”,则(﹣n,﹣m) “同心有理数对”(填“是”或“不是”),说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展“我的中国梦”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.

(1)根据如图,分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析哪个班级5名选手的复赛成绩波动小?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点A,B,C是数轴上的三个点,其中AB=12,且A,B两点表示的数互为相反数.
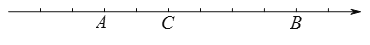
(1)请在数轴上标出原点O,并写出点A表示的数;
(2)如果点Q以每秒2个单位的速度从点B出发向左运动,那么经过 秒时,点C恰好是BQ的中点;
(3)如果点P以每秒1个单位的速度从点A出发向右运动,那么经过多少秒时PC=2PB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理,但远在毕达哥拉斯出生之前,这一定理早已被人们所利用,世界上各个文明古国都对勾股定理的发现和研究作出过贡献(希腊、中国、埃及、巴比伦、印度等),特别是定理的证明,据说有400余种方法.其中在《几何原本》中有一种证明勾股定理的方法:如图所示,作CG⊥FH,垂足为G,交AB于点P,延长FA交DE于点S,然后将正方形ACED、正方形BCNM作等面积变形,得S正方形ACED=SACQS,S正方形BCNM=SBCQT,这样就可以完成勾股定理的证明.对于该证明过程,下列结论错误的是( )
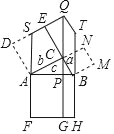
A. △ADS≌△ACB B. SACQS=S矩形APGF
C. SCBTQ=S矩形PBHG D. SE=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是昌平区2019年1月份每天的最低和最高气温,观察此图,下列说法正确的是( )

A.在1月份中,最高气温为10℃,最低气温为-2℃
B.在10号至16号的气温中,每天温差最小为7℃
C.每天的最高气温均高于0℃,最低气温均低于0℃
D.每天的最高气温与最低气温都是具有相反意义的量
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由一个角为60°且边长为1的菱形组成的网格,每个菱形的顶点称为格点,点A,B,C都在格点上,则tan∠BAC=_____.

相关试题

