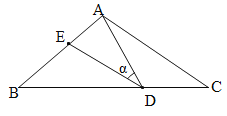
【题目】如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=![]() .有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或
.有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或![]() ;④0<BE≤
;④0<BE≤![]() ,其中正确的结论是 (填入正确结论的序号).
,其中正确的结论是 (填入正确结论的序号).
参考答案:
【答案】②③.
【解析】
试题分析:∵∠ADE=∠B=∠α,∠EAD=∠EAD,∴△ADE∽△ABD,而△ABD不一定相似△ACD,故①不正确;
过A作AF⊥BC于F,如图1,∵AB=AC,∴BF=FC,∵tan∠α=![]() ,∠B=∠α,∴tanB=
,∠B=∠α,∴tanB=![]() ,∴cosB=
,∴cosB=![]() ,∴
,∴![]() ,∴BF=
,∴BF=![]() AB=12,∴BC=24,∵DC=9,∴BD=BC-DC=15,∴BD=AC,∵AB=AC,∴∠B=∠C,∴∠α=∠C,∵∠C+∠CAD=∠α+∠BDE,∴∠BDE=∠CAD,在△BED和△CDA中,∵∠BDE=∠CAD,BD=AC,∠B=∠C,∴△BDE≌△CAD,故②正确;
AB=12,∴BC=24,∵DC=9,∴BD=BC-DC=15,∴BD=AC,∵AB=AC,∴∠B=∠C,∴∠α=∠C,∵∠C+∠CAD=∠α+∠BDE,∴∠BDE=∠CAD,在△BED和△CDA中,∵∠BDE=∠CAD,BD=AC,∠B=∠C,∴△BDE≌△CAD,故②正确;

若△BDE为直角三角形,则有两种情况:(1)若∠BED=90°,∵∠BDE=∠CAD,∠B=∠C,∴△BDE∽△CAD,∴∠CDA=∠BED=90°,∴AD⊥BC,∵AB=AC,∴BD=![]() BC=12;
BC=12;
(2)若∠BDE=90°,如图2,设BD=x,则DC=24-x,∵∠CAD=∠BDE=90°,∠B=∠C=∠α,∴cos∠C=cosB=![]() ,∴
,∴![]() ,解得:
,解得:![]() ,∴若△BDE为直角三角形,则BD为12或
,∴若△BDE为直角三角形,则BD为12或![]() ,故③正确;
,故③正确;

设BE=x,CD=y,∵△BDE∽△CAD,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴0<BE≤
,∴0<BE≤![]() ,∴故④错误;
,∴故④错误;
故答案为:②③.
-
科目: 来源: 题型:
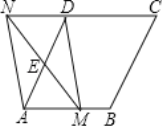
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数. -
科目: 来源: 题型:
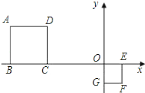
查看答案和解析>>【题目】正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),则这两个正方形的位似中心的坐标为 .
-
科目: 来源: 题型:
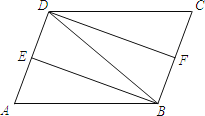
查看答案和解析>>【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次三项式x2﹣2(m+1)x+16是一个完全平方式,那么m的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,

(1)请画出平移后的图形△A′B′C′;
(2)并写出△A′B′C′各顶点的坐标;
(3)求出△A′B′C′的面积.
相关试题

