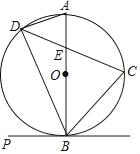
【题目】如图,C、D是以AB为直径的⊙O上的点,![]() ,弦CD交AB于点E.
,弦CD交AB于点E.
(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2﹣CE2=CEDE;
(3)已知OA=4,E是半径OA的中点,求线段DE的长.
参考答案:
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
(1)由AB是⊙O的直径知∠BAD+∠ABD=90°,由PB是⊙O的切线知∠PBD+∠ABD=90°,据此可得答案;
(2)连接OC,设圆的半径为r,则OA=OB=OC=r,证△ADE∽△CBE得DECE=AEBE=r2-OE2,由![]() 知∠AOC=∠BOC=90°,根据勾股定理知CE2=OE2+r2、BC2=2r2,据此得BC2-CE2=r2-OE2,从而得证;
知∠AOC=∠BOC=90°,根据勾股定理知CE2=OE2+r2、BC2=2r2,据此得BC2-CE2=r2-OE2,从而得证;
(3)先求出BC=4![]() 、CE=2
、CE=2![]() ,根据BC2-CE2=CEDE计算可得.
,根据BC2-CE2=CEDE计算可得.
(1)∵AB是⊙O的直径,
∴∠ADB=90°,即∠BAD+∠ABD=90°,
∵PB是⊙O的切线,
∴∠ABP=90°,即∠PBD+∠ABD=90°,
∴∠BAD=∠PBD;
(2)∵∠A=∠C、∠AED=∠CEB,
∴△ADE∽△CBE,
∴![]() ,即DECE=AEBE,
,即DECE=AEBE,
如图,连接OC,

设圆的半径为r,则OA=OB=OC=r,
则DECE=AEBE=(OA﹣OE)(OB+OE)=r2﹣OE2,
∵![]() ,
,
∴∠AOC=∠BOC=90°,
∴CE2=OE2+OC2=OE2+r2,BC2=BO2+CO2=2r2,
则BC2﹣CE2=2r2﹣(OE2+r2)=r2﹣OE2,
∴BC2﹣CE2=DECE;
(3)∵OA=4,
∴OB=OC=OA=4,
∴BC=![]() =4
=4![]() ,
,
又∵E是半径OA的中点,
∴AE=OE=2,
则CE=![]() =
=![]() =2
=2![]() ,
,
∵BC2﹣CE2=DECE,
∴(4![]() )2﹣(2
)2﹣(2![]() )2=DE2
)2=DE2![]() ,
,
解得:DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是反比例函数y=
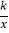 图象上一点,PM∥x轴交y轴于点M,MP=2,点Q的坐标为(4,0),连接PO、PQ,△OPM的面积为3,求该反比例函数的表达式是△OPQ的面积.
图象上一点,PM∥x轴交y轴于点M,MP=2,点Q的坐标为(4,0),连接PO、PQ,△OPM的面积为3,求该反比例函数的表达式是△OPQ的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣
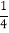 <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)
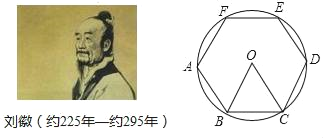
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师请同学们思考如下问题:
请利用直尺和圆规四等分弧AB.
小亮的作法如下:
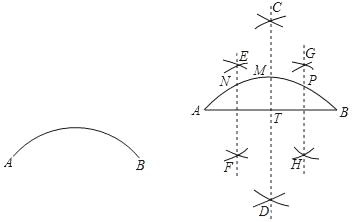
如图,
(1)连接AB;
(2)作AB的垂直平分线CD交弧AB于点M.交AB于点T;
(3)分别作线段AT,线段BT的垂直平分线EF,GH,交弧AB于N,P两点;
那么N,M,P三点把弧AB四等分.
老师问:“小亮的作法正确吗?”
请回备:小亮的作法_____(“正确”或“不正确”)理由是_____.
相关试题

