【题目】【阅读材料】
小明在学习二次根式时,发现一些含根号的式子可以化成另一式子的平方.如:
5+2![]() =(2+3)+2
=(2+3)+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() =(
=(![]() )2;
)2;
8+2![]() =(3+5)+2
=(3+5)+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() =(
=(![]() )2.
)2.
【类比归纳】
(1)请你仿照小明的方法将9+2![]() 化成一个式子的平方;
化成一个式子的平方;
(2)将下列等式补充完整:a+b+2![]() =( )2(a≥0,b≥0),并证明这个等式;
=( )2(a≥0,b≥0),并证明这个等式;
【变式探究】
(3)若a+2![]() =(
=(![]() )2,且a,m,n均为正整数,则a= .
)2,且a,m,n均为正整数,则a= .
参考答案:
【答案】(1) (![]() )2;(2)见解析;(3)11或13或17或31
)2;(2)见解析;(3)11或13或17或31
【解析】试题分析:(1)利用完全平方公式可得;
(2)利用完全平方公式求解;
(3)把等式右边展开即可得到m+n=a,mn=30,则利用整数的特征得到mn=1×30=15×2=5×6=10×3,于是可得m+n的值.
试题解析:
(1)9+2![]() =(7+2)+2
=(7+2)+2![]() =(
=(![]() )2+(
)2+(![]() )2+2
)2+2![]() =(
=(![]() )2.
)2.
(2) ![]() .
.
证明:右边=(![]() )2+2
)2+2![]() +(
+(![]() )2=a+b+2
)2=a+b+2![]() =左边,
=左边,
所以a+b+2![]() =(
=(![]() )2.
)2.
(3)∵a+2![]() =(
=(![]() )2,(
)2,(![]() )2=m+n+2
)2=m+n+2![]() ,
,
∴m+n=a,mn=30,
又∵30=1×30=15×2=5×6=10×3,
∴m+n=31或17或11或13.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
-
科目: 来源: 题型:
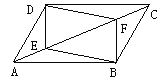
查看答案和解析>>【题目】如图,□ABCD中,点E、F在对角线AC上,且AE=CF。求证:四边形BEDF是平行四边形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家超市同价销售同一款可拆分式驱蚊器,1套驱蚊器由1个加热器和1瓶电热蚊香液组成.电热蚊香液作为易耗品可单独购买,1瓶电热蚊香液的售价是1套驱蚊器的
 .已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
.已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.(1)求1套驱蚊器和1瓶电热蚊香液的售价;
(2)为了促进该款驱蚊器的销售,甲超市打8.5折销售,而乙超市采用的销售方法是顾客每买1套驱蚊器送1瓶电热蚊香液.在这段促销期间,甲超市销售2000套驱蚊器,而乙超市在驱蚊器销售上获得的利润不低于甲超市的1.2倍.问乙超市至少销售多少套驱蚊器?
-
科目: 来源: 题型:
查看答案和解析>>【题目】发现与探索。
(1)根据小明的解答将下列各式因式分解

① a2-12a+20;②(a-1)2-8(a-1)+7;③ a2-6ab+5b2
(2)根据小丽的思考解决下列问题:

①说明:代数式a2-12a+20的最小值为-16.
②请仿照小丽的思考解释代数式-(a+1)2+8的最大值为8,并求代数式-a2+12a-8的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】模型与应用.
(模型)
(1)如图①,已知AB∥CD,求证∠1+∠MEN+∠2=360°.

(应用)
(2)如图②,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6的度数为 .
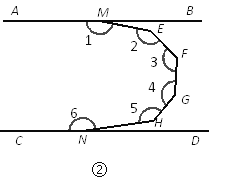
如图③,已知AB∥CD,则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为 .

(3)如图④,已知AB∥CD,∠AM1M2的角平分线M1 O与∠CMnMn-1的角平分线MnO交于点O,若∠M1OMn=m°.

在(2)的基础上,求∠2+∠3+∠4+∠5+∠6+……+∠n-1的度数.(用含m、n的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的三条角平分线相交于点O,过点O作EF∥BC,分别交AB于E,交AC于F,则图中的等腰△有( )个

(A)4(B)5
(C)6(D)7
相关试题

