搜索
【题目】如图，等边△ABC的三条角平分线相交于点O，过点O作EF∥BC，分别交AB于E，交AC于F，则图中的等腰△有（ ）个
(A)4(B)5
(C)6(D)7
参考答案：
【答案】D
【解析】根据角平分线的性质和等边三角形的性质就可以求出角相等，利用角相等根据等腰三角形的判定定理究竟可以求出图中的等腰三角形的个数，从而得出答案．
解：∵△ABC是等边三角形，
∴∠ABC=∠ACB=∠BAC
∵等边△ABC的三条角平分线相交于点O，
∴∠1=∠2=∠3=∠4=∠7=∠8=30°，
∵EF∥BC，
∴∠4=∠5=30°，∠7=∠8=30°，∠9=∠ABC=60°，∠10=∠ACB=60°．
∴∠9=∠10，∠3=∠5，∠6=∠7．
∴△BEO，△CFO，△BOC，△AOB，△AOC，△AEF，△ABC是等腰三角形，共有7个．
故选D．
本题考查了等边三角形的性质，角平分线的定义，平行线的性质，等腰三角形的判定．
-
科目： 来源： 题型：
查看答案和解析>>【题目】【阅读材料】
小明在学习二次根式时,发现一些含根号的式子可以化成另一式子的平方.如:
5+2
=(2+3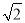)+2
=(
)2+(
)2+2
=(
)2;8+2
=(3+5)+2
=(
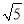)2+(
)2+2
=(
)2.【类比归纳】
(1)请你仿照小明的方法将9+2
化成一个式子的平方;(2)将下列等式补充完整:a+b+2
=( )2(a≥0,b≥0),并证明这个等式;【变式探究】
(3)若a+2
=(
)2,且a,m,n均为正整数,则a= . -
科目： 来源： 题型：
查看答案和解析>>【题目】发现与探索。
（1）根据小明的解答将下列各式因式分解
① a2－12a＋20；②（a－1）2－8（a－1）＋7；③ a2－6ab＋5b2
（2）根据小丽的思考解决下列问题：
①说明：代数式a2－12a＋20的最小值为－16．
②请仿照小丽的思考解释代数式－（a＋1）2＋8的最大值为8，并求代数式－a2＋12a－8的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】模型与应用.
（模型）
（1）如图①，已知AB∥CD，求证∠1＋∠MEN＋∠2＝360°.
（应用）
（2）如图②，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6的度数为 ．
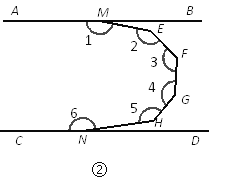
如图③，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6＋…＋∠n的度数为 ．
（3）如图④，已知AB∥CD，∠AM1M2的角平分线M1 O与∠CMnMn－1的角平分线MnO交于点O，若∠M1OMn＝m°．
在（2）的基础上，求∠2+∠3+∠4+∠5+∠6＋……＋∠n－1的度数．（用含m、n的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB＝AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E，F，则下列四个结论：①AD上任意一点到点C，B的距离相等；②AD上任意一点到AB，AC的距离相等；③BD＝CD，AD⊥BC；④∠BDE＝∠CDF.其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】按图中方式用火柴棒搭正方形
①搭1个正方形需要 根火柴棒；
②搭2个正方形需要 根火柴棒，搭3个正方形需要 根火柴棒；
③搭10个这样的正方形需要多少根火柴棒；
④搭100个这样的正方形需要多少根火柴棒？
⑤如果用x表示所搭正方形的个数，那么搭x个这样的正方形需要多少根火柴棒？与同伴交流。
⑥根据你的计算方法，搭200个这样的正方形需要多少根火柴棒？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，线段AB＝8cm，C是线段AB上一点，AC＝3.2cm，M是AB的中点，N是AC的中点．
(1)求线段CM的长；
(2)求线段MN的长．
相关试题
