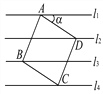
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1.如果正方形ABCD的四个顶点分别在四条直线上,那么sinα=_.
参考答案:
【答案】![]()
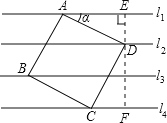
【解析】过D作EF⊥l1,交l1于E,交l4于F,
∵EF⊥l1,l1∥l2∥l3∥l4,
∴EF和l2,l3,l4的夹角都是90°,
即EF与l2,l3,l4都垂直,
∴DE=1,DF=2.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=CD,
∴∠ADE+∠CDF=90°,
又∵∠α+∠ADE=90°,
∴∠α=∠CDF,
∵AD=CD,∠AED=∠DFC=90°,
∴△ADE≌△DCF,
∴DE=CF=1,
∴在Rt△CDF中,CD=![]() ,
,
∴sinα=sin∠CDF=![]() ,
,
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数

100
150
200
500
800
1000
摸到白球的次数

58
96
116
295
484
601
摸到白球的频率

0.58
0.64
0.58
0.59
0.605
0.601
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在E处,BE与AD相交于点F,下列结论:
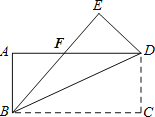
①BD=AD2+AB2;②△ABF≌△EDF;③
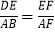 ;④AD=BD cos45°.其中正确的一组是( )
;④AD=BD cos45°.其中正确的一组是( )A. ①② B. ②③ C. ①④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1.
(2)作出△ABC关于原点O成中心对称的△A1B2C2.
(3)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的弦CD与直径AB垂直于F,点E在CD上,且AE=CE.

(1)求证:CA2=CE CD;
(2)已知CA=5,EC=3,求sin∠EAF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在△CFE中,CF=6,CE=12,∠FCE=45°,以点C为圆心,以任意长为半径作AD,再分别以点A和点D为圆心,大于
 AD长为半径做弧,交EF于点B,AB∥CD.
AD长为半径做弧,交EF于点B,AB∥CD.
(1)求证:四边形ACDB为△CFE的亲密菱形;
(2)求四边形ACDB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 分别与x轴、y轴交于
分别与x轴、y轴交于 两点,与直线
两点,与直线 交于点C(4,2).
交于点C(4,2).(1)点A坐标为( , ),B为( , );
(2)在线段
 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形 是平行四边形;
是平行四边形;(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得
 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
相关试题

