【题目】直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)
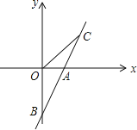
(1)求直线AB所对应的函数关系式;
(2)若直线AB上一点C在第一象限且点C的坐标为(a,2),求△BOC的面积.
参考答案:
【答案】(1)y=2x-2
(2)2
【解析】
(1)设直线AB的解析式为y=kx+b,将A(1,0),B(0,-2)分别代入解析式组成方程组,求k,b,从而得到解析式;(2)以OB为底,C到OB的垂线段长为高,根据三角形面积公式即可求解.
(1)解:设直线AB解析式为y=kx+b(k≠0)
将A(1,0),B(0,-2)代入,得
![]()
解得:![]()
∴直线AB的解析式为y=2x-2

(2)解:∵C(a,2)在图象上,
∴2=2a-2
∴a=2, ∴C(2,2)
过点C作CH⊥x轴,垂足为H,如图
∴CH=2
∴△BOC的面积为![]() ·OB·CH=
·OB·CH=![]() ×2×2=2
×2×2=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连接DE,交AB于点O,若BC=8,AO=
 ,求cos∠AED的值.
,求cos∠AED的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,线段AM为BC边上的高.动点D在射线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.

(1)填空:∠ACB=______度;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动点D在射线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按
 元
元 计;B类收费标准如下:没有月租费,但通话费按
计;B类收费标准如下:没有月租费,但通话费按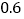 元
元 计
计 按照此类收费标准完成下列各题:
按照此类收费标准完成下列各题: 直接写出每月应缴费用
直接写出每月应缴费用 元
元 与通话时长
与通话时长 分
分 之间的关系式:
之间的关系式:A类:______B类:______
 若每月平均通话时长为300分钟,选择______类收费方式较少.
若每月平均通话时长为300分钟,选择______类收费方式较少. 求每月通话多长时间时,按
求每月通话多长时间时,按 两类收费标准缴费,所缴话费相等.
两类收费标准缴费,所缴话费相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )
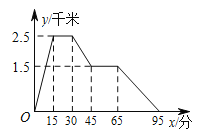
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=
 , AD=4.
, AD=4.
(1)求BC的长;
(2)求tan∠DAE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB⊥BD,sinA=
 ,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=
,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y= (k>0)同时经过B、D两点,则点B的坐标是_____.
(k>0)同时经过B、D两点,则点B的坐标是_____.
相关试题

