【题目】如图,在等腰Rt△ABC中,∠ACB=90![]() ,D为BC边上的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF.
,D为BC边上的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.

参考答案:
【答案】(1) 答案见解析;(2) 答案见解析
【解析】试题分析:
(1)由已知条件证:∠BDE=∠BFE=45°,从而可得:BF=BD,结合点D是CB的中点,可得BF=BD=CD;然后结合已知条件证:△ACD≌△CBF,从而可得:∠CAD=∠BCF,结合∠CAD+∠CDA=90![]() ,可得∠BCF+∠CDA=90
,可得∠BCF+∠CDA=90![]() ,这样就可得:∠AGC=90
,这样就可得:∠AGC=90![]() ,从而可得:AD⊥CF;
,从而可得:AD⊥CF;
(2)由(1)中BF=BD结合DE⊥AB可证:AB垂直平分DF,由此可得:AD=AF;由△ACD≌△CBF可得:AD=CF;两者结合可得:AF=CF,因此△ACF是等腰三角形.
试题解析:
(1)∵在等腰Rt△ABC中,∠ACB=90![]() ,
,
∴∠CBA=45![]() ,AC=BC .
,AC=BC .
又∵BF//AC, ∠ACB=90![]() ,
,
∴∠FBC=90![]() ,
,
∴∠FBE=45![]() .
.
又∵DE⊥AB,
∴∠BFE=45°,∠BDE=45°,
∴∠BFE=∠BDE,
∴BF=BD ,
∵D为BC的中点,
∴BD=CD,
∴ BF=CD.
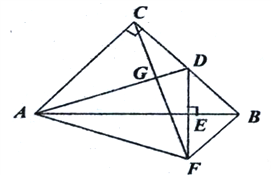
在△ACD和△CBF中, 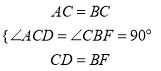 ,
,
∴ △ACD≌△CBF,
∴∠CAD=∠BCF,
又∵ ∠CAD+∠CDA=90![]() ,
,
∴∠BCF+∠CDA=90![]() ,
,
∴∠AGC=90![]() ,即AD⊥CF .
,即AD⊥CF .
(2)△ACF是等腰三角形,理由如下:
由(1)可知:△ACD≌△CBF;BD=BF,DE![]() AB,
AB,
∴CF=AD;DE=FE,
∴AB垂直平分DF,
∴AD=AF,
∴AF=CF ,
∴△ACF是等腰三角形.
-
科目: 来源: 题型:
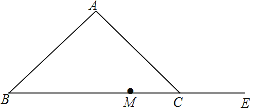
查看答案和解析>>【题目】如图,在△ABC中,AB=AC.
(1)尺规作图:作∠ABC的平分线,交AC于点D(保留作图痕迹,不写作法);
(2)E是底边BC的延长线上一点,M是BE的中点,连接DE,DM,若CE=CD,求证:DM⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC与∠ACB的平分线相交于点O.过点O作EF∥BC.分别交AB和AC于点E、F.
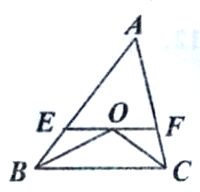
(l)你能发现哪些结论,把它们写出来.并选择一个加以证明;
(2)若AB=10,AC=8.试求△AFF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实数m满足(m-2018)2+(2019-m)2=15,则(m-2018)(2019-m)值是( )
A. 0 B. 1 C. -7 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】为建设“美丽乡村”,需要对某村居民的自来水管进行改造,该工程若由甲队单独施工恰好在规定时间内完成;若由乙队单独施工,则完成工程所需时间是规定天数的1.5倍如果由甲、乙两队先合做10天,那么余下的工程由乙队单独完成还需5天.
(1)这项工程完成规定的时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3600元,为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合做来完成,则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断中错误的是( )
A. 有两角和其中一个角的对边对应相等的两个三角形全等
B. 有一边相等的两个等边三角形全等
C. 有两边和一角对应相等的两个三角形全等
D. 有两边和其中一边上的中线对应相等的两个三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题发现:
(
 )如图①,点
)如图①,点 和点
和点 均在⊙
均在⊙ 上,且
上,且 ,点
,点 和点
和点 均在射线
均在射线 上,若
上,若 ,则点
,则点 与⊙
与⊙ 的位置关系是__________;若
的位置关系是__________;若 ,则点
,则点 与⊙
与⊙ 的位置关系是__________.
的位置关系是__________.问题解决:
如图②,图③所示,四边形
 中,
中,  ,
,  ,
,  ,且
,且 ,
,  ,点
,点 是
是 边上任意一点.
边上任意一点.(
 )当
)当 时,求
时,求 的长度.
的长度.(
 )是否存在点
)是否存在点 ,使得
,使得 最大?若存在,请说明理由,并求出
最大?若存在,请说明理由,并求出 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.


相关试题

