【题目】如图,在ABCD中,对角线AC,BD相交于O,E,F是对角线上的两点,给出下列四个条件:①OE=OF;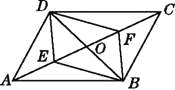
②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个
B.1个
C.2个
D.3个
参考答案:
【答案】B
【解析】解:①∵ABCD,∴OB=OD
∵OE=OF
∴四边形DEBF是平行四边形,因此①不符合题意;
②DE=BF不能判断四边形DEBF是平行四边形,因此②符合题意;
③∵ABCD,
∴AD=BC,AD∥BC
∴∠DAE=∠BCF
在△ADE和△BCF中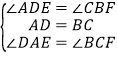
∴△ADE≌△BCF
∴DE=BF,∠DEA=∠BFC
∴∠DEA+∠DEO=180°,∠BFC+∠OFB=180°
∴∠DEO=∠OFB
∴DE∥BF DE=BF
∴四边形DEBF是平行四边形,因此③不符合题意;
④当∠ABE=∠CDF,与③的证明方法一样,可证出四边形DEBF是平行四边形,因此④不符合题意;
因此不能判定四边形DEBF是平行四边形只有②。
故答案为:B
利用平行四边形的性质及判断和全等三角形的性质及判断,逐一判断即可得出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系第一象限内,直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,点C在直线y=2x上:CB的延长线交直线y=x于点A1,作等腰Rt△A1B1C1,是∠A1B1C1=90°,B1C1∥x轴,A1B1∥y轴,点C1在直线y=2x上…按此规律,则等腰Rt△AnBnCn的腰长为______.
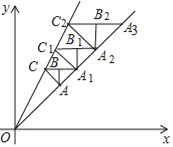
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,对角线AC,BD相交于点O,给出下列四组条件:
①AB∥CD,AD∥BC;
②AB=CD,AD=BC;
③AO=CO,BO=DO;
④AB∥CD,AD=BC.
其中一定能判定这个四边形是平行四边形的条件有( )
A.1组
B.2组
C.3组
D.4组 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,BC=3,AB=4,D是边AB上一点,DE∥BC交AC于点E,将△ADE沿DE翻折得到△A′DE,若△A′EC是直角三角形,则AD长为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲商品每件20元,乙商品每件15元,若购买甲、乙两种商品共40件,恰好用去675元,求甲、乙商品各买多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)、B(5,0)两点,与y轴交于C点,D为抛物线的顶点,E为抛物线上一点,且C、E关于抛物线的对称轴对称,分别作直线AE、DE.
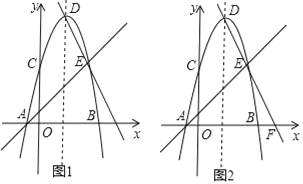
(1)求此二次函数的关系式;
(2)在图1中,直线DE上有一点Q,使得△QCO≌△QBO,求点Q的坐标;
(3)如图2,直线DE与x轴交于点F,点M为线段AF上一个动点,有A向F运动,速度为每秒2个单位长度,运动到F处停止,点N由F处出发,沿射线FE方向运动,速度为每秒
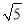 个单位长度,M、N两点同时出发,运动时间为t秒,当M停止时点N同时停止运动坐标平面内有一个动点P,t为何值时,以P、M、N、F为顶点的四边形是特殊的平行四边形.请直接写出t值.
个单位长度,M、N两点同时出发,运动时间为t秒,当M停止时点N同时停止运动坐标平面内有一个动点P,t为何值时,以P、M、N、F为顶点的四边形是特殊的平行四边形.请直接写出t值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树情况进行了调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
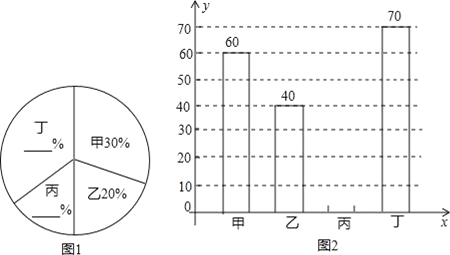
(1)这四个班共植树 棵;
(2)补全两幅统计图;
(3)求图1中“甲”班级所对应的扇形圆心角的度数;
(4)若四个班级所种植的树成活了190棵,全校共植树2000棵,请你估计全校种植的树中成活的树有多少棵.
相关试题

