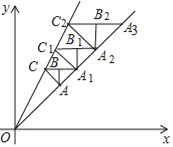
【题目】如图,在平面直角坐标系第一象限内,直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,点C在直线y=2x上:CB的延长线交直线y=x于点A1,作等腰Rt△A1B1C1,是∠A1B1C1=90°,B1C1∥x轴,A1B1∥y轴,点C1在直线y=2x上…按此规律,则等腰Rt△AnBnCn的腰长为______.
参考答案:
【答案】![]()
【解析】设AB=a,
∵直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,
∴C(,1﹣a,1+a),
∵点C在直线y=2x上,
∴1+a=2(1﹣a),
解得a=![]() ,
,
∴等腰Rt△ABC的腰长为![]() ,
,
∴C(![]() ,
, ![]() ),
),
∴A1的坐标为(![]() ,
, ![]() ),
),
设A1B1=b,则C1(![]() ﹣b,
﹣b, ![]() +b),
+b),
∵点C1在直线y=2x上,
∴![]() +b=2(
+b=2(![]() ﹣b)
﹣b)
解得b=![]() ,
,
∴等腰Rt△A1B1C1的腰长为![]()
∴C1(![]() ,
, ![]() )
)
∴A2(![]() ,
, ![]() ),
),
设A2B2=c,则C2(![]() ﹣c,
﹣c, ![]() +c),
+c),
∵点C2在直线y=2x上,
∴![]() +c=2(
+c=2(![]() ﹣c),
﹣c),
解得c=![]() ,
,
∴等腰Rt△A2B2C2的腰长为![]() ,
,
以此类推,
A3B3=![]() ,即等腰Rt△A3B3C3的腰长为
,即等腰Rt△A3B3C3的腰长为![]() ,
,
A4B4=![]() ,即等腰Rt△A4B4C4的腰长为
,即等腰Rt△A4B4C4的腰长为![]() ,
,
…
∴AnBn=![]() ,等腰Rt△AnBnCn的腰长为
,等腰Rt△AnBnCn的腰长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣
 x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.(1)用b的代数式表示顶点M的坐标;
(2)当tan∠MAN=2时,求此二次函数的解析式及∠ACB的正切值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一,目前我国每年可利用的淡水资源总量为27500亿米3 , 人均占有淡水量居全世界第110位,因此我们要节约用水,27500亿用科学记数法表示为( )
A.275×104
B.2.75×104
C.2.75×1012
D.27.5×1011 -
科目: 来源: 题型:
查看答案和解析>>【题目】下了各式运算正确的是( )
A.2(a﹣1)=2a﹣1
B.a2b﹣ab2=0
C.2a3﹣3a3=a3
D.a2+a2=2a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,对角线AC,BD相交于点O,给出下列四组条件:
①AB∥CD,AD∥BC;
②AB=CD,AD=BC;
③AO=CO,BO=DO;
④AB∥CD,AD=BC.
其中一定能判定这个四边形是平行四边形的条件有( )
A.1组
B.2组
C.3组
D.4组 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,BC=3,AB=4,D是边AB上一点,DE∥BC交AC于点E,将△ADE沿DE翻折得到△A′DE,若△A′EC是直角三角形,则AD长为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC,BD相交于O,E,F是对角线上的两点,给出下列四个条件:①OE=OF;
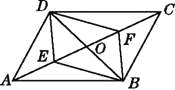
②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个
B.1个
C.2个
D.3个
相关试题

