【题目】问题探究:
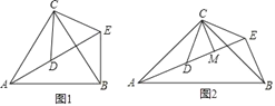
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求出∠AEB的度数以及判断线段CM、AE、BE之间的数量关系,并说明理由.
参考答案:
【答案】探究展示:(1)证明见解析; (2)600.
拓展延伸:(1)∠AEB=900 ;(2)AE= 2CM+BE,理由见解析.
【解析】试题分析:问题探究:(1)先证出∠ACD=∠BCE,那么△ACD≌△BCE,根据全等三角形证出AD=BE;
(2)∠ADC=∠BEC,求出∠ADC=120°,得出∠BEC=120°,从而证出∠AEB=60°;
问题变式:证明△ACD≌△BCE,得出∠ADC=∠BEC、AD=BE,从而得到∠AEB的度数,再由等腰直角三角形的性质得到DM=ME=CM即可.
试题解析:问题探究:
(1) ∵△ACB和△DCE均为等边三角形,∴∠ACB=∠DCE=60°,AC=BC、DC=EC,∴∠ACD=∠BCE,∴△CDA≌△CEB, ∴AD=BE
(2)∵△CDA≌△CEB,∴∠CEB=∠CDA=1200,又∠CED=600,∴∠AEB=1200-600=600.
问题变式:
(1)∵△ACB和△DCE均为等腰直角三角形,∠ACB =∠DCE= 900,
∴AC=BC, CD=CE,
∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD= ∠BCE
∴△ACD≌△BCE
∴AD = BE, ∠BEC=∠ADC=1350.
∴∠AEB=∠BEC-∠CED=1350-450=900
(2)AE= 2CM+BE
在等腰直角三角形DCE中,CM为斜边DE上的高,
∴CM= DM= ME,∴DE=2CM.
∴AE=DE+AD=2CM+BE
∴AE= 2CM+BE
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(2mx2+7x2-1)-(5x2-6x+8) 化简后不含x2 项.求多项式3m3+(5m3-2m-3) 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段 AB上的点数与线段的总数有如下关系:如果线段上有3个点时,线段共有3条;如果线段上有4个点时,线段共有6条;如果线段上有5个点时,线段共有10条;
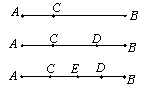
(1)当线段上有6个点时,线段共有条?
(2)当线段上有n个点时,线段共有多少条?(用n的代数式表示)
(3)当n=100时,线段共有多少条? -
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,为了山更绿、水更清,某区大力实施生态修复工程,发展林业产业,确保到2021年实现全区森林覆盖率达到72.6%的目标.已知该区2019年全区森林覆盖率为60%,设从2019年起该区森林覆盖率年平均增长率为x,则x=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形三边所在直线距离相等的点有__________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑车从家出发,先向东骑行1km到达A村,继续向东骑行4km到达B村,然后向西骑行8km到达C村,最后回到家.
(1)以家为原点,以向东方向为正方向,用1 cm表示1 km,画出数轴,并在数轴上表示出A、B、C三个村的位置;
(2)C村离A村有多远?
(3)小明一共骑行了多少千米? -
科目: 来源: 题型:
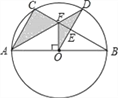
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2
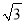 .
.(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
相关试题

