Question

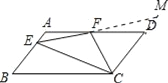
【题目】如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，联结EF、CF，那么下列结论中一定成立的个数是（　　）

①∠DCF=∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】C

【解析】由在平行四边形ABCD中，AD=2AB，F是AD的中点，易得AF=FD=CD，继而证得①∠DCF=∠BCD；然后延长EF，交CD延长线于M，分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF（ASA），得出对应线段之间关系进而得出答案．

解：①∵F是AD的中点，

∴AF=FD，

∵在ABCD中，AD=2AB，

∴AF=FD=CD，

∴∠DFC=∠DCF，

∵AD∥BC，

∴∠DFC=∠FCB，

∴∠DCF=∠BCF，

∴∠DCF=∠BCD，故此选项正确；

②延长EF，交CD延长线于M，

∵四边形ABCD是平行四边形，

∴AB∥CD，

∴∠A=∠MDF，

∵F为AD中点，

∴AF=FD，

在△AEF和△DFM中，

，

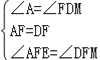∴△AEF≌△DMF（ASA），

∴FE=MF，∠AEF=∠M，

∵CE⊥AB，

∴∠AEC=90°，

∴∠AEC=∠ECD=90°，

∵FM=EF，

∴FC=FM，故②正确；

③∵EF=FM，

∴S△EFC=S△CFM，

∵MC＞BE，

∴S△BEC＜2S△EFC

故S△BEC=2S△CEF错误；

④设∠FEC=x，则∠FCE=x，

∴∠DCF=∠DFC=90°﹣x，

∴∠EFC=180°﹣2x，

∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x，

∵∠AEF=90°﹣x，

∴∠DFE=3∠AEF，故此选项正确．

故选C．