【题目】如图,E、F是ABCD对角线AC上两点,AE=CF. 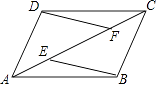
(1)求证:△ABE≌△CDF;
(2)连结DE,BF,求证:四边形DEBF是平行四边形.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中, 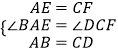 ,
,
∴△ABE≌△CDF(SAS)
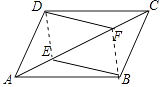
(2)证明:连接DE、BF,如图所示:
由(1)得:△ABE≌△CDF,
∴BE=DF,
同理:DE=BF,
∴四边形DEBF是平行四边形.
【解析】(1)由平行四边形的性质得出∠BAE=∠DCF,由SAS证明△ABE≌△CDF即可;(2)由全等三角形的性质得出BE=DF,同理:DE=BF,即可得出结论.
【考点精析】通过灵活运用平行四边形的判定与性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三对某班最近一次数学测验成绩(得分取整数)进行统计分析,将所有成绩由低到高分成五组,并绘制成如图的频数分布直方图,请结合直方图提供的信息,回答下列问题:
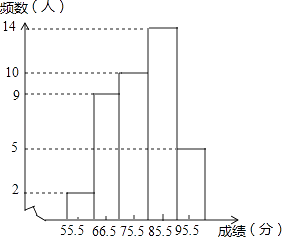
(1)该班共有名同学参加这次测验;
(2)这次测验成绩的中位数落在分数段内;
(3)若该校一共有800名初三学生参加这次测验,成绩80分以上(不含80分)为优秀,估计该校这次数学测验的优秀人数是多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果+20%表示增加20%,那么﹣8%表示( )
A. 减少8%B. 减少20%C. 增加20%D. 增加8%
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程或方程组:
(1)
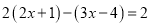 ; (2)
; (2)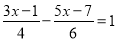 ;
;(3)
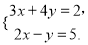
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动,设动点运动时间为t秒.
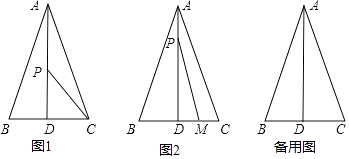
(1)求AD的长.
(2)当P、C两点的距离为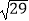 时,求t的值.
时,求t的值.
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在时刻t,使得S△PMD=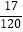 S△ABC?若存在,请求出t的值;若不存在,请说明理由.
S△ABC?若存在,请求出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段FG∥x轴,则此段时间,甲机器人的速度为 米/分;
(4)求A、C两点之间的距离;
(5)直接写出两机器人出发多长时间相距28米.

相关试题

