【题目】如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动,设动点运动时间为t秒.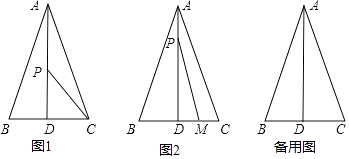
(1)求AD的长.
(2)当P、C两点的距离为 ![]() 时,求t的值.
时,求t的值.
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在时刻t,使得S△PMD= ![]() S△ABC?若存在,请求出t的值;若不存在,请说明理由.
S△ABC?若存在,请求出t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵AB=AC=13,AD⊥BC,
∴BD=CD=5cm,且∠ADB=90°,
∴AD2=AC2﹣CD2
∴AD=12cm
(2)
解:AP=t,
∴PD=12﹣t,
在Rt△PDC中,PC= ![]() ,CD=5,根据勾股定理得,PC2=CD2+PD2,
,CD=5,根据勾股定理得,PC2=CD2+PD2,
∴29=52+(12﹣t)2,
∴t=10或t=14(舍).
即:t的值为10s
(3)
解:假设存在t,使得S△PMD= ![]() S△ABC.
S△ABC.
∵BC=10,AD=12,
∴S△ABC= ![]() BC×AD=60,
BC×AD=60,
① 若点M在线段CD上,
即 0≤t< ![]() 时,PD=12﹣t,DM=5﹣2t,
时,PD=12﹣t,DM=5﹣2t,
由S△PMD= ![]() S△ABC,
S△ABC,
即 ![]() (12﹣t)(5﹣2t)=
(12﹣t)(5﹣2t)= ![]() ,
,
2t2﹣29t+43=0
解得t1= ![]() (舍去),t2=
(舍去),t2= ![]()
② 若点M在射线DB上,即 ![]() <t<12.
<t<12.
由S△PMD= ![]() S△ABC
S△ABC
得 ![]() (12﹣t)(2t﹣5)=
(12﹣t)(2t﹣5)= ![]() ,
,
2t2﹣29t+77=0
解得 t=11或t= ![]()
综上,存在t的值为 ![]() s或 11s或
s或 11s或 ![]() s,使得S△PMD=
s,使得S△PMD= ![]() S△ABC
S△ABC
【解析】(1)根据等腰三角形性质和勾股定理解答即可;(2)根据勾股定理建立方程求解即可;(3)根据题意列出PD、MD的表达式解方程组,由于M在D点左右两侧情况不同,所以进行分段讨论即可,注意约束条件.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程或方程组:
(1)
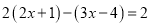 ; (2)
; (2)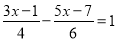 ;
;(3)
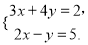
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F是ABCD对角线AC上两点,AE=CF.
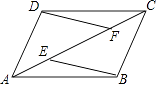
(1)求证:△ABE≌△CDF;
(2)连结DE,BF,求证:四边形DEBF是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段FG∥x轴,则此段时间,甲机器人的速度为 米/分;
(4)求A、C两点之间的距离;
(5)直接写出两机器人出发多长时间相距28米.

-
科目: 来源: 题型:
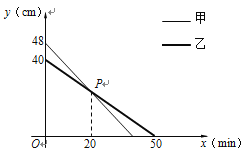
查看答案和解析>>【题目】同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y(cm)与燃烧时间x(min)的关系如图所示.
(1)求乙蜡烛剩下的长度y与燃烧时间x的函数表达式;
(2)求点P的坐标,并说明其实际意义;
(3)求点燃多长时间,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.
-
科目: 来源: 题型:
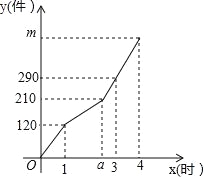
查看答案和解析>>【题目】某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
(1)甲车间每小时生产产品 件,a= .
(2)求乙车间更换新设备之后y与x之间的函数关系式,并求m的值.
(3)若乙车间在开始更换新设备时,增加两名工作人员,这样可便更换设备时间减少0.5小时,并且更换后工作效率提高到原来的2倍,那么两个车间完成原任务量需几小时?
相关试题

