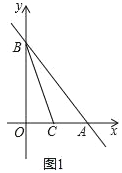
【题目】在平面直角坐标系中,点O为坐标原点,直线y=﹣![]() x+12与x轴,y轴分别相交于点A,B,∠ABO的平分线与x轴相交于点C.
x+12与x轴,y轴分别相交于点A,B,∠ABO的平分线与x轴相交于点C.
(1)如图1,求点C的坐标;
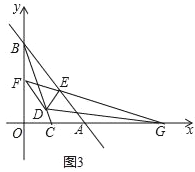
(2)如图2,点D,E,F分别在线段BC,AB,OB上(点D,E,F都不与点B重合),连接DE,DF,EF,且∠EDF+∠OBC=90°,求证:∠FED=∠AED;
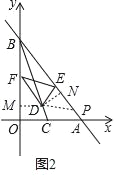
(3)如图3,在(2)的条件下,延长线段FE与x轴相交于点G,连接DG,若∠CGD=∠FGD,BF:BE=5:8,求直线DF的解析式.

参考答案:
【答案】(1)点C坐标为(4,0);(2)见解析;(3)直线DF的解析式为y=﹣![]() x+7.
x+7.
【解析】整体分析:
(1)作CH⊥AB于H,由△OBC≌△HBC求BH,解Rt△ACH,求CH,即得OC;(2)过点D分别作DM⊥y轴于点M,DN⊥AB于点N,在NA上截取NP=FM,连接PD,用SAS证△DFM≌△DPN,得DF=DP,∠EDF=∠EDP,证△DEF≌△DEP;(3)过点F作FQ⊥BE于点Q,过点D作DM⊥y轴于M,DN⊥AB于N,DR⊥EF于R,DS⊥OG于点S,过点A作AT⊥BC交BC的延长线于T,连接AD.解Rt△ACT求ST,AT,∠ADT=∠DAT=45°,求DC,从而得DS,OS,求出D的坐标,判断DF∥AB,即可求DF的解析式.
解:(1)如图1,作CH⊥AB于H.

由题意A(9,0),B(0,12),
在Rt△AOB中,AB=![]() =
=![]() =15,tan∠OAB=
=15,tan∠OAB=![]() =
=![]() =
=![]() ,
,
∵∠CBH=∠CBO,∠CHB=∠COB,CB=CB,
∴△OBC≌△HBC,
∴BH=OB=12,OC=CH,AH=15﹣12=3,
在Rt△ACH中,tan∠CAH=![]() =
=![]() ,
,
∠CH=4,
∴OC=CH=4,
∴点C坐标为(4,0).
(2)解:如图2,过点D分别作DM⊥y轴于点M,DN⊥AB于点N,在NA上截取NP=FM,连接PD.
∵∠EDF+∠OBC=90°,∠BDM+∠OBC=90°,
∴∠EDF=∠BDM,同理∠BDN=∠BDM=![]() ∠MDN,
∠MDN,
∴∠EDF=![]() ∠MDN,
∠MDN,
∵∠DBM=∠DBN,DM⊥OB,DN⊥AB,
∴DM=DN,
∵∠FMD=∠PND=90°,NP=FM,
∴△DFM≌△DPN,
∴DF=DP,∠FDM=∠PDN,
∴∠FDM+∠FDN=∠PDN+∠FDN,即∠FDP=∠MDN,
∴∠EDF=![]() ∠FDP=∠EDP,
∠FDP=∠EDP,
∵DE=DE,
∴△DEF≌△DEP,
∴∠FED=∠AED.
(3)解:如图3,过点F作FQ⊥BE于点Q,过点D作DM⊥y轴于M,DN⊥AB于N,DR⊥EF于R,DS⊥OG于点S,过点A作AT⊥BC交BC的延长线于T,连接AD.
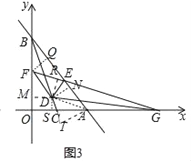
∵∠DEF=∠DEA,DR⊥EF,DN⊥EA,
∴DR=DN,同理DR=DS,
∴DN=DS,
∴∠BAD=∠OAD,同理∠OFD=∠DFG,
在Rt△ACT中,AC=9﹣4=5,tan∠ACT=tan∠BCO=![]() =3,
=3, ![]() =3,
=3,
设CT=m,则AT=3m.
∵CT2+AT2=AC2,
∴m2+(3m)2=52,
解得m=![]() 或﹣
或﹣![]() (舍),
(舍),
∴CT=![]() ,AT=
,AT=![]() ,
,
∵∠ADC=∠ABD+∠BAD=![]() (∠OBA+∠BAO)=
(∠OBA+∠BAO)=![]() ×90°=45°,
×90°=45°,
∴∠DAT=45°=∠ADC,
∴DT=AT=![]() ,
,
∴CD=DT﹣CT=![]() ,同理可得,CS=1,DS=3=OM,
,同理可得,CS=1,DS=3=OM,
∴OS=4﹣1=3,
∴点D坐标(3,3),
设BF=5n,则BE=8n,在Rt△BFQ中,cos∠FBQ=![]() =
=![]() =
=![]() ,
,
∴BQ=4n=EQ,
∴FQ⊥AB,∠BFQ=∠EFQ,
∴∠DFQ=∠DFC+∠EFQ=![]() (∠OFG+∠BFE)=
(∠OFG+∠BFE)=![]() ×180°=90°,
×180°=90°,
∴∠DFQ=∠BQF=90°,
∴DF∥AB,
设直线DF的解析式为y=﹣![]() x+b,
x+b,
∴3=﹣![]() ×3+b,
×3+b,
解得b=7,
∴直线DF的解析式为y=﹣![]() x+7.
x+7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】701班小强买了张100元的深圳通乘车卡,如果他乘车的次数用
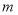 表示,则记录他每次乘车后的余额n (元)如下表:
表示,则记录他每次乘车后的余额n (元)如下表: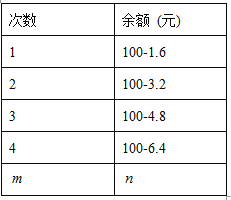
(1)写出余额n与乘车的次数m的关系式.
(2)利用上述关系式计算小强乘了23次车还剩下多少元?
(3)小强最多能乘几次车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B分别为数轴上的两点,点A表示的数是﹣30,点B表示的数是50.

(1)请写出A、B两点间的距离是 .
(2)现有一只蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左移动,同时另一只蚂蚁Q恰好从点A出发,以每秒2个单位长度的速度沿数轴向右移动,设两只蚂蚁在数轴上的点C相遇.求两只蚂蚁在数轴上的点C相遇时所用的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题
(1)“绿水青山就是金山银山”,某省2018年新建湿地公园和森林公园共42个,其中森林公园比湿地公园多4个.问该省2018年新建湿地公园和森林公园各多少个?
(2)某市大市场进行高端的家用电器销售,每件电器的进价是2000元,若按标价的八折销售该电器一件,则利润率为20%.求:
①该电器的标价是多少元?
②现如果按同一标价的九折销售该电器一件,那么获得的利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中, ,
, 是对角线
是对角线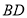 上不同的两点,连接
上不同的两点,连接 ,
, ,
,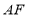 ,
,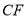 .下列条件中,不能得出四边形
.下列条件中,不能得出四边形 一定是平行四边形的为( )
一定是平行四边形的为( )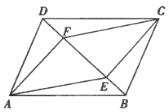
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,……以此类推,则a2018的值为( )
A. ﹣1007 B. ﹣1008 C. ﹣1009 D. ﹣2018
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是_____海里(不近似计算).

相关试题

