【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)BC=2CD,理由见解析.
【解析】
(1)利用矩形的性质,即可判定△FAE≌△CDE,即可得到CD=FA,再根据CD∥AF,即可得出四边形ACDF是平行四边形;
(2)先判定△CDE是等腰直角三角形,可得CD=DE,再根据E是AD的中点,可得AD=2CD,依据AD=BC,即可得到BC=2CD.
(1)∵四边形ABCD是矩形,
∴AB∥CD,
∴∠FAE=∠CDE,
∵E是AD的中点,
∴AE=DE,
又∵∠FEA=∠CED,
∴△FAE≌△CDE,
∴CD=FA,
又∵CD∥AF,
∴四边形ACDF是平行四边形;
(2)BC=2CD.
证明:∵CF平分∠BCD,
∴∠DCE=45°,
∵∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CD=DE,
∵E是AD的中点,
∴AD=2CD,
∵AD=BC,
∴BC=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1,有以下四个结论:
①abc>0;②b2﹣4ac>0;③b=﹣2a;④a+b+c>2,
其中正确的是(填写序号)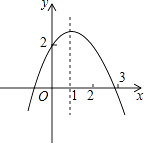
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是平行四边形,点A,B,C在⊙O上,P为
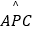 上一点,连接AP,CP,求∠P的度数.
上一点,连接AP,CP,求∠P的度数. 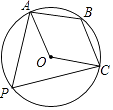
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,D为AB的中点,四边形BCED为平行四边形,DE,AC相交于F.连接DC,AE.
(1)试确定四边形ADCE的形状,并说明理由.
(2)若AB=16,AC=12,求四边形ADCE的面积.
(3)当△ABC满足什么条件时,四边形ADCE为正方形?请给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
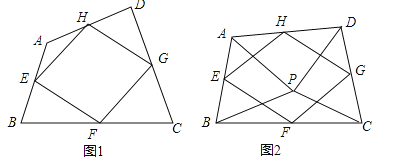
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
相关试题

