【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
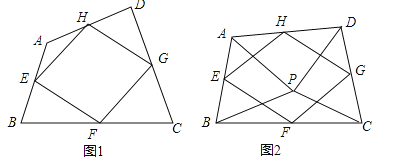
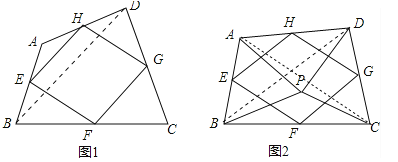
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
参考答案:
【答案】(1)证明见解析;(2)四边形EFGH是菱形;(3)四边形EFGH是正方形.
【解析】
试题分析:(1)如图1中,连接BD,根据三角形中位线定理只要证明EH∥FG,EH=FG即可.
(2)四边形EFGH是菱形.先证明△APC≌△BPD,得到AC=BD,再证明EF=FG即可.
(3)四边形EFGH是正方形,只要证明∠EHG=90°,利用△APC≌△BPD,得∠ACP=∠BDP,即可证明∠COD=∠CPD=90°,再根据平行线的性质即可证明.
试题解析:(1)证明:如图1中,连接BD.
∵点E,H分别为边AB,DA的中点,∴EH∥BD,EH=![]() BD,∵点F,G分别为边BC,CD的中点,∴FG∥BD,FG=
BD,∵点F,G分别为边BC,CD的中点,∴FG∥BD,FG=![]() BD,∴EH∥FG,EH=GF,∴中点四边形EFGH是平行四边形.
BD,∴EH∥FG,EH=GF,∴中点四边形EFGH是平行四边形.
(2)四边形EFGH是菱形.
证明:如图2中,连接AC,BD.
∵∠APB=∠CPD,∴∠APB+∠APD=∠CPD+∠APD,即∠APC=∠BPD,在△APC和△BPD中,∵AP=PB,∠APC=∠BPD,PC=PD,∴△APC≌△BPD,∴AC=BD.∵点E,F,G分别为边AB,BC,CD的中点,∴EF=![]() AC,FG=
AC,FG=![]() BD,∵四边形EFGH是平行四边形,∴四边形EFGH是菱形.
BD,∵四边形EFGH是平行四边形,∴四边形EFGH是菱形.
(3)四边形EFGH是正方形.
证明:如图2中,设AC与BD交于点O.AC与PD交于点M,AC与EH交于点N.
∵△APC≌△BPD,∴∠ACP=∠BDP,∵∠DMO=∠CMP,∴∠COD=∠CPD=90°,∵EH∥BD,AC∥HG,∴∠EHG=∠ENO=∠BOC=∠DOC=90°,∵四边形EFGH是菱形,∴四边形EFGH是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b的图象经过第一、三、四象限,则( )
A. k>0,b>0B. k>0,b<0C. k<0,b>0D. k<0,b<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|m﹣3|+(n+2)2=0,则m+2n的值为( )
A. ﹣1 B. 1 C. 4 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】投影可分为________和________;一个立体图形,共有________种视图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数图象经过点A(5,3),且与直线y=2x﹣3平行,则这个一次函数的解析式为( )
A.y=2x﹣7B.y=2x+7C.y=﹣2x﹣7D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的重心是三角形中( )
A. 三条高的交点 B. 三条中线的交点
C. 三条角平分线的交点 D. 三边垂直平分线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华家冰箱冷冻室的温度为-5℃,调低6℃后的温度为( ).
A. 4℃ B. -11℃ C. -1℃ D. 11℃
相关试题

