搜索
【题目】(本题10分) (湖南湘西24,10分)如图,已知矩形ABCD的两条对角线相交于O,∠ACB=30°,AB=2.
(1)求AC的长.
(2)求∠AOB的度数.
(3)以OB、OC为邻边作菱形OBEC,求菱形OBEC的面积.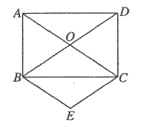
参考答案：
【答案】解(1)在矩形ABCD中,∠ABC=90°,
∴Rt△ABC中, ∠ACB=30°,
∴AC=2AB=4.
(2)在矩形ABCD中,
∴AO=OA=2,
又∵AB=2,
∴△AOB是等边三角形,
∴∠AOB=60°.
(3)由勾股定理,得BC=
,
.
,所以菱形OBEC的面积是2
.
【解析】
解 (1)在矩形ABCD中,∠ABC=90°,
∴Rt△ABC中, ∠ACB=30°,
∴AC=2AB=4.
(2)在矩形ABCD中,
∴AO=OA=2,
又∵AB=2,
∴△AOB是等边三角形,
∴∠AOB=60°.
(3)由勾股定理,得BC=,
.
,所以菱形OBEC的面积是2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，有一个菱形BFDE（点E，F分别在线段AB，CD上），记它们的面积分别为SABCD和SBFDE ， 现给出下列命题：①若
= 
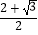，则tan∠EDF= 
；②若DE2=BDEF，则DF=2AD，则（ ） 
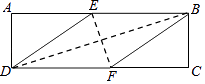
A.①是假命题，②是假命题
B.①是真命题，②是假命题
C.①是假命题，②是真命题
D.①是真命题，②是真命题 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形OABC中，点B(4，4)，点E，F分别在边BC，BA上，OE=
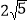，若∠EOF=45°，则OF的解析式为 ( )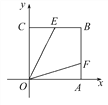
A. y=
x B. y=
x C. y=
x D. y=
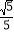x -
科目： 来源： 题型：
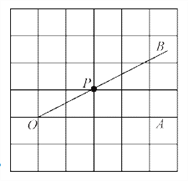
查看答案和解析>>【题目】如图，在
的正方形网格中，点P是
的边OB上的一点．（1）过点P画OB的垂线，交OA于点C；过点P画OA的垂线，垂足为H；
（2）线段PH的长度是点P到直线__________的距离；
（3）线段__________的长度是点C到直线OB的距离；
（4）线段PC、PH、OC这三条线段大小关系是__________（用“<”号连接）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校计划在总费用2300元的限额内，租用客车送234名学生和6名教师集体外出活动，每辆客车上至少要有1名教师.现有甲、乙两种大客车，它们的载客量和租金如下表所示.
甲种客车
乙种客车
载客量/(人/辆)
45
30
租金/(元/辆)
400
280
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据要求完成下列题目：
（1）如图中有________块小正方体；
（2） 请在下面方格纸中分别画出它的左视图和俯视图（画出的图都用铅笔涂上阴影）；
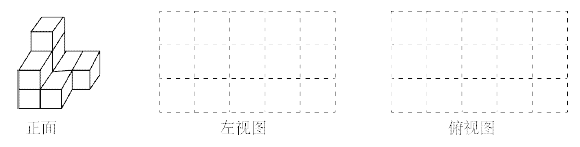
（3）用小正方体搭一个几何体，使得它的俯视图和左视图与你在上图方格中所画的图一致，则这样的几何体最少要________个小正方体，最多要________个小正方体.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本小题满分8分）某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷数量收取印刷费.甲乙两厂的印刷费用y（千元）与证书数量x（千个）的函数关系图象分别如图中甲、乙所示.
(1) 请你直接写出甲厂的制版费及y甲与x的函数解析式，并求出其证书印刷单价.
(2) 当印制证书8千个时，应选择哪个印刷厂节省费用，节省费用多少元？
(3) 如果甲厂想把8千个证书的印制工作承揽下来，在不降低制版费的前提下，每个证书最少降低多少元？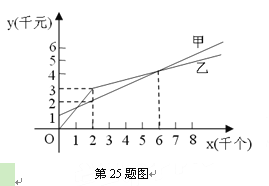
相关试题
