【题目】如图,正方形OABC中,点B(4,4),点E,F分别在边BC,BA上,OE=![]() ,若∠EOF=45°,则OF的解析式为 ( )
,若∠EOF=45°,则OF的解析式为 ( )
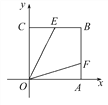
A. y=![]() x B. y=
x B. y=![]() x C. y=
x C. y=![]() x D. y=
x D. y=![]() x
x
参考答案:
【答案】B
【解析】作辅助线,构建全等三角形,证明△OCE≌△OAD和△EOF≌△DOF,得EF=FD,设AF=x,在直角△EFB中利用勾股定理列方程求出x=![]() ,根据正方形的边长写出点F的坐标,并求直线OF的解析式.
,根据正方形的边长写出点F的坐标,并求直线OF的解析式.
延长BF至D,使AD=CE,连接OD.
∵四边形OABC是正方形,∴OC=OA,∠OCB=∠OAD,∴△OCE≌△OAD,∴OE=OD,∠COE=∠AOD.
∵∠EOF=45°,∴∠COE+∠FOA=90°﹣45°=45°,∴∠AOD+∠FOA=45°,∴∠EOF=∠FOD.
∵OF=OF,∴△EOF≌△DOF,∴EF=FD,由题意得:OC=4,OE=2![]() ,∴CE=
,∴CE=![]() =2,∴BE=2,设AF=x,则BF=4﹣x,EF=FD=2+x,∴(2+x)2=22+(4﹣x)2,解得:x=
=2,∴BE=2,设AF=x,则BF=4﹣x,EF=FD=2+x,∴(2+x)2=22+(4﹣x)2,解得:x=![]() ,∴F(4,
,∴F(4,![]() ),设OF的解析式为:y=kx,4k=
),设OF的解析式为:y=kx,4k=![]() ,k=
,k=![]() ,∴OF的解析式为:y=
,∴OF的解析式为:y=![]() x.
x.
故选B.

-
科目: 来源: 题型:
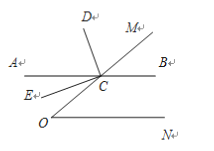
查看答案和解析>>【题目】已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:

下列说法正确的是( )
A.这10名同学体育成绩的中位数为38分
B.这10名同学体育成绩的平均数为38分
C.这10名同学体育成绩的众数为39分
D.这10名同学体育成绩的方差为2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别为SABCD和SBFDE , 现给出下列命题:①若
 =
= 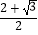 ,则tan∠EDF=
,则tan∠EDF=  ;②若DE2=BDEF,则DF=2AD,则( )
;②若DE2=BDEF,则DF=2AD,则( ) 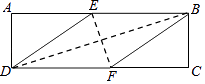
A.①是假命题,②是假命题
B.①是真命题,②是假命题
C.①是假命题,②是真命题
D.①是真命题,②是真命题 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
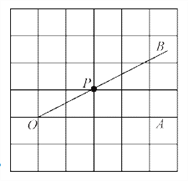
 的正方形网格中,点P是
的正方形网格中,点P是 的边OB上的一点.
的边OB上的一点.(1)过点P画OB的垂线,交OA于点C;过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到直线__________的距离;
(3)线段__________的长度是点C到直线OB的距离;
(4)线段PC、PH、OC这三条线段大小关系是__________(用“<”号连接).
-
科目: 来源: 题型:
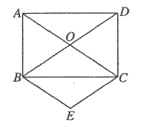
查看答案和解析>>【题目】(本题10分) (湖南湘西24,10分)如图,已知矩形ABCD的两条对角线相交于O,∠ACB=30°,AB=2.
(1)求AC的长.
(2)求∠AOB的度数.
(3)以OB、OC为邻边作菱形OBEC,求菱形OBEC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车
乙种客车
载客量/(人/辆)
45
30
租金/(元/辆)
400
280
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
相关试题

