【题目】如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F. 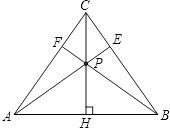
(1)证明:∠CAE=∠CBF;
(2)证明:AE=BF;
(3)以线段AE,BF和AB为边构成一个新的三角形ABG(点E与点F重合于点G),记△ABC和△ABG的面积分别为S△ABC和S△ABG , 如果存在点P,能使得S△ABC=S△ABG , 求∠ACB的取值范围.
参考答案:
【答案】
(1)证明:∵△ABC是等腰三角形,CH是底边上的高线,
∴AC=BC,∠ACP=∠BCP.
又∵CP=CP,
∴△ACP≌△BCP.
∴∠CAP=∠CBP,即∠CAE=∠CBF.
(2)证明:∵在△ACE与△BCF中,
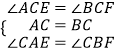 ,
,
∴△ACE≌△BCF(ASA).
∴AE=BF.
(3)解:∵由(2)知△ABG是以AB为底边的等腰三角形,
∴S△ABC=S△ABG.
∴AE=AC.
①当∠ACB为直角或钝角时,在△ACE中,不论点P在CH何处,均有AE>AC,所以结论不成立;
②当∠ACB为锐角时,∠CAH=90°﹣ ![]() ∠ACB,而∠CAE<∠CAH,要使AE=AC,只需使∠ACB=∠CEA,
∠ACB,而∠CAE<∠CAH,要使AE=AC,只需使∠ACB=∠CEA,
此时,∠CAE=180°﹣2∠ACB,
只须180°﹣2∠ACB<90°﹣ ![]() ∠ACB,
∠ACB,
解得:60°<∠ACB<90°.
【解析】(1)证得△ACP≌△BCP即可;(2)加上(1)的结论,证得△ACE≌△BCF即可;(3)假设存在点P,能使得S△ABC=S△ABG , 由(2)得到的AE=BF,则新三角形ABG也为等腰三角形,根据底边都为AB,面积相等,得到高相等,所以AC=AE,即三角形ACE为等腰三角形,则底角∠ACB为锐角,即可得到∠ACB的取值范围.
【考点精析】关于本题考查的等腰三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平移变换不仅和几何图形联系密切,而且在汉字中也存在着平移变换现象.如:“林”“田”“众”.请你开动脑筋,写出三个可由平移变换得到的汉字:________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条平行直线被第三条直线所截,其中一组同旁内角之差为90°,则这两个角的度数分别是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列是一名同学做的6道练习题:①(﹣3)0=1;②a3+a3=a6;③(﹣a5)÷(﹣a3)=﹣a2;④4m﹣2=
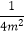 ;⑤(xy2)3=x3y6;⑥22+23=25 , 其中做对的题有( )
;⑤(xy2)3=x3y6;⑥22+23=25 , 其中做对的题有( )
A.1道
B.2道
C.3道
D.4道 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.

(1)如图1,求证:∠B=∠C;
(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;
(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商厦进货员预测一种应季衬衫能畅销市场,就用0.8万元购进这种衬衫,面市后果然供不应求.于是,商厦又用1.76万元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了4元,商厦销售这种衬衫时每件预定售价都是58元.
(1)求这种衬衫原进价为每件多少元?
(2)经过一段时间销售,根据市场饱和情况,商厦经理决定对剩余的100件衬衫进行打折销售,以提高回款速度,要使这两批衬衫的总利润不少于6300元,最多可以打几折?
相关试题

