【题目】已知数轴上点A对应的数是20,点B对应的数是﹣30,甲从A点出发以每秒1个单位长度的速度匀速运动,乙从B出发以每秒3个长度单位的速度匀速运动,若甲乙两人同时出发
(1)若甲和乙在数轴上运动3秒后,
①它们相距最远时,甲所在的位置对应的数是 ,乙所在的位置对应的数是
②它们距离最近时,甲所在的位置对应的数是 ,乙所在的位置对应的数是
(2)若甲和乙同时向右,出发多少秒后,甲和乙相距20个长度单位?
(3)若甲和乙进行匀速往返跑训练,甲从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点……;乙从B点起跑,到达A点后,立即转身跑向B点,到达B点后,又立即转身跑向A点……;两人同时出发,问:起跑后两人第二次相遇的时间是多少?

参考答案:
【答案】(1)①23,-39;②-21,17;(2)15或35;(3)37.5s
【解析】
(1)①当它们相距最远时,甲和乙背道而驰,即甲沿数轴正方向爬行,乙沿数轴负方向爬行,由此分别求出它们所在的位置对应的数;②当它们相距最近时,乙追赶甲,它们同向而行,即甲和乙都沿数轴正方向爬行,由此分别求出它们所在的位置对应的数;
(2)分两种情况进行讨论;
(3)第二次相遇时,两人路程和是3×50=150.
∵甲从A点出发以每秒1个单位长度的速度爬行,乙从B点出发以每秒3个单位长度的速度运动,若它们同时出发运动3秒,∴甲运动路程:1×3=3,
乙运动路程:3×3=9,
①当它们相距最远时,甲和乙背道而驰,即甲沿数轴正方向爬行,乙沿数轴负方向爬行,
此时甲所在的位置对应的数为20+3=23,乙所在的位置对应的数为309=39;
②当它们相距最近时,乙追赶甲,它们同向而行,即甲和乙都沿数轴正方向爬行,此时甲所在的位置对应的数为20-3=17,乙所在的位置对应的数为30+9=-21.
(2)设t秒后,甲和乙相距20个长度单位.
由题意可知,当乙未追上甲,S甲=t,S乙=3t,
![]() S乙-S甲=50-20,
S乙-S甲=50-20,
即3t-t=30,得t=15.
当乙追上甲并超过甲20个单位时,S乙-S甲=50+20
即3t-t=70,得t=35.
![]() 当t=15或35.
当t=15或35.
(3)设x秒时两人第二次相遇,
(3+1)x=3×50
x=37.5(s)
答:第二次相遇时需要37.5s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,请你观察下列几种简单多面体模型,解答下列问题:

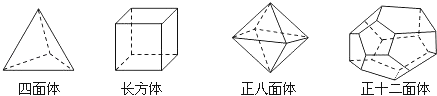
图1 图2
(探索新知)如图1,(1)根据上面多面体模型,完成表格中的空格;
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
6
12
正八面体
8
12
正十二面体
20
12
30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)根据以上关系式猜想是否存在一个多面体,它有16个面,50条棱,34个顶点?并写出理由。
(实际应用)如图2,足球一般有32块黑白皮子缝合而成,黑色的是正五边形,白色的是正六边形,如
果我们近似把足球看成一个多面体.
(1)设黑色的正五边形有x块,则白色的正六边形有(32﹣x)块,当把足球看成一个多面体时,它的棱数是 ,它的顶点数是 .
(2)求出黑皮和白皮各有多少块?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=9,AB的垂直平分线交BC与点M,AC的垂直平分线交BC于点N,则△AMN的周长=_____.

-
科目: 来源: 题型:
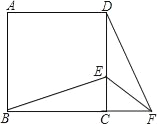
查看答案和解析>>【题目】如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠BEC=60°,求∠EFD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )

A. 88° B. 30° C. 32° D. 48°
-
科目: 来源: 题型:
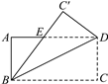
查看答案和解析>>【题目】如图所示,将长方形ABCD沿直线BD折叠,使点C落在点C′处,BC′交AD于点E,AD=16,AB=8,求DE的长.
相关试题

