【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(﹣1,0)、C(0,﹣3)两点,与x轴交于另一点B.
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标.
参考答案:
【答案】
(1)
解:设抛物线的解析式为y=ax2+bx+c,
则有:  ,
,
解得:  ,
,
所以抛物线的解析式为y=x2﹣2x﹣3
(2)
解:令x2﹣2x﹣3=0,解得x1=﹣1,x2=3,所以B点坐标为(3,0).
设直线BC的解析式为y=kx+b,
则 ![]() ,
,
解得 ![]() ,
,
所以直线解析式是y=x﹣3.
当x=1时,y=﹣2.
所以M点的坐标为(1,﹣2)
【解析】(1)利用待定系数设抛物线的解析式为y=ax2+bx+c,代入求出即可;(2)根据令x2﹣2x﹣3=0,解得x1=﹣1,x2=3,所以B点坐标为(3,0),进而求出直线BC的解析式,即可得出M点的坐标.
-
科目: 来源: 题型:
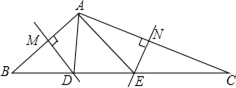
查看答案和解析>>【题目】如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAC=120°,求∠DAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.求证:

(1)△AEF≌△BEC;
(2)四边形BCFD是平行四边形. -
科目: 来源: 题型:
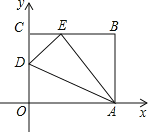
查看答案和解析>>【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.
(1)求证:四边形ACED是平行四边形;
(2)若AC=2,CE=4,求四边形ACEB的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时. 为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,

请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)户外活动时间的众数和中位数分别是多少?
(4)若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?
-
科目: 来源: 题型:
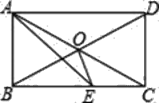
查看答案和解析>>【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15° .
(1)求证:△AOB为等边三角形;
(2)求∠BOE度数.
相关试题

