搜索
【题目】如图，AB是⊙O的直径，弦BC=9，∠BOC=50°，OE⊥AC，垂足为E．
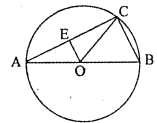
（1）求OE的长．
（2）求劣弧AC的长(结果精确到0．1)．
参考答案：
【答案】（1）4.5（2）24.2
【解析】（1）∵OE⊥AC，OE为直径的一部分
∴AE=EC （2分）
又∵AO=BO
∴
（2分）
（2）∵∠COB=50°
∴∠AOC=130° （1分）
∵AO=CO，OE⊥AC
∴∠AOE=
∠AOC =65°（2分）
∴
∴AO=
（1分）
∴
（2分）
（1）由垂径定理知，由E是AC的中点，点O是AB的中点，则OB是△ABC的BC边对的中位线，所以OE=BC÷2；
（2）由圆周角定理得，∠A=∠BDC=25°，由等边对等角得∠OCA=∠A，由三角形内角和定理求得∠AOC的度数，再利用弧长公式求得弧AC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】灌云教育局为了解今年九年级学生体育测试情况，随机抽查了部分学生的体育测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制成如下的统计图，请你结合图中所给信息解答下列问题：
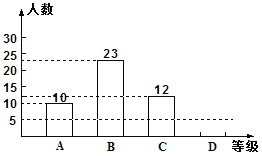
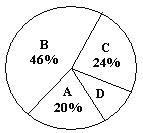
（说明：A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下）
（1）请把条形统计图补充完整；
（2）样本中D级的学生人数占全班学生人数的百分比是_____________；
（3）扇形统计图中A级所在的扇形的圆心角度数是_____________；
（4）若该县九年级有8000名学生，请你用此样本估计体育测试中A级和B级的学生人数之和．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两超市(大型商场)同时开业，为了吸引顾客，都举行了有奖酬宾活动：凡购物满100元，均可得到一次摸奖的机会. 在一个纸盒里装有2个红求和2个白球，除颜色外其他都相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券(在他们超市使用时，与人民币等值)的多少（如下表）
甲 超 市
球
两红
一红一白
两白
礼金券
5
10
5
乙 超 市
球
两红
一红一白
两白
礼金券
10
5
10
（1）用树状图或列表法表示得到一次摸奖机会时中礼金券的所有情况；
（2）如果只考虑中奖因素，你将会选择去哪个超市购物？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某建筑工地计划租用甲、乙两辆车清理建筑垃圾，已知甲车单独运完需要15天，乙车单独运完需要30天．甲车先运了3天，然后甲、乙两车合作运完剩下的垃圾．
（1）甲、乙两车合作还需要多少天运完垃圾？
（2）已知甲车每天的租金比乙车多100元，运完垃圾后建筑工地共需支付租金3950元．则甲、乙车每天的租金分别为多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一次数学课上，王老师出示一道题：解方程
．小马立即举手并在黑板上写出了解方程过程，具体如下：解：
，去括号，得：
．………………①移项，得：
．…………………②合并同类项，得：
．……………………③系数化为1，得：
．………………………④（1）请你写出小马解方程过程中哪步错了，并简要说明错误原因；
（2）请你正确解方程：
． -
科目： 来源： 题型：
查看答案和解析>>【题目】美丽的洪泽湖周边景点密布.如图A，B为湖滨的两个景点，C为湖心一个景点.景点B在景点C的正东，从景点A看，景点B在北偏东75°方向，景点C在北偏东30°方向.一游客自景点
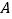驾船以每分钟20米的速度行驶了10分钟到达景点C，之后又以同样的速度驶向景点B，该游客从景点C到景点B需用多长时间（精确到1分钟）？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠BAC=45°，若BD=2，CD=3，AD⊥BC于D，将△ABD沿AB所在的直线折叠，使点D落在点E处；将△ACD沿AC所在的直线折叠，使点D落在点F处，分别延长EB、FC使其交于点M．
(1)判断四边形AEMF的形状，并给予证明．
(2)设AD=x，利用勾股定理，建立关于x的方程模型，求四边形AEMF的面积.
相关试题
