【题目】综合题
(1)如图1,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE交于F,连DE,求证:DFDA=DBDC;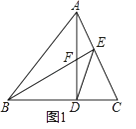
(2)如图2,若∠BAC=90°,AD⊥BC于D,F为线段AD上一点,在AD延长线上找一点G使AD2=DFDG,请画出图形找出点G并加以证明;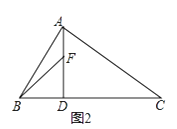
(3)如图3,在(1)的条件下,若∠ABC=45°,EF=1,EC=3,直接写出BD长.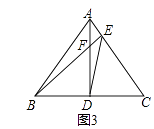
参考答案:
【答案】
(1)解:证明:如图1中,
∵AD、AE是△ABC的高,
∴∠ADC=∠BDF=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
∴△DBF∽△DAC,
∴ ![]() =
= ![]() ,
,
∴DFDA=DBDC.
(2)解:如图2中,在DC上截取DM,使得DM=DA,
连接FM、AM,作MN⊥FM交AD的延长线于G.则AD2=DFDG.
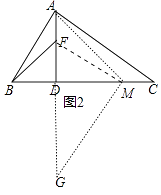
理由:∵∠MDF=∠MDG=∠FMG=90°,
∴∠DMF+∠DMG=90°,∠DMG+∠G=90°,
∴∠DMF=∠G,
∴△DMF∽△DGM,
∴ ![]() =
= ![]() ,
,
∴DM2=DFDG,
∵AD=DM,
∴AD2=DFDG.
(3)解:如图3中,连接FC.
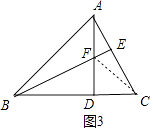
∵∠ABC=45°,∠ADB=90°,
∴BD=AD,
∵∠DBF=∠CAD(已证),∠BDF=∠ADC=90°,
∴△BDF≌△ADC,
∴DF=DC,
在Rt△EFC中,FC= ![]() =
= ![]() =
= ![]() ,
,
∴DF=DC= ![]() ,设BD=AD=y,则AC=
,设BD=AD=y,则AC= ![]() =
= ![]() ,
,
∵△EAF∽△DAC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得y=2 ![]() 或
或 ![]() (舍弃),
(舍弃),
∴BD=2 ![]() .
.
【解析】(1)先证明∠DBF=∠DAC,然后再证明△DBF∽△DAC,最后,依据相似三角形对应边成比例求解即可;
(2)在DC上截取DM,使得DM=DA,连接FM、AM,作MN⊥FM交AD的延长线于G.则AD2=DFDG.接下来,再证明△DMF∽△DGM即可解决问题;
(3)连接FC.依据ASA可证明△BDF≌△ADC,根据全等三角形的性质定理可得到DF=DC,接下来,依据勾股定理可求得DF、DC的长,设BD=AD=y,则可得到AC的长,最后,依据△EAF∽△DAC,可得到关于y的比例式,从而可求得y的值.
【考点精析】掌握相似三角形的应用是解答本题的根本,需要知道测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分; B:49-45分;C:44-40分;D:39-30分;E:29-0分).每段包含最高分,不包含最低分,统计表如下,统计图如图所示.
分数段
频数(人)
百分比













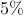

根据上面提供的信息,回答下列问题:
(1)在统计表中,
 的值为___,
的值为___,  的值为__,并将统计图补充完整.
的值为__,并将统计图补充完整.(2)成绩在40分以上定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知I是△ABC的内心,AI延长线交△ABC外接圆于D,连BD.

(1)在图1中,求证:DB=DI;
(2)如图2,若AB为直径,且OI⊥AD于I点,DE切圆于D点,求sin∠ADE的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b与反比例函数y=
 交于A(﹣1,2),B(2,n),与y轴交于C点.
交于A(﹣1,2),B(2,n),与y轴交于C点.
(1)求反比例函数和一次函数解析式;
(2)如图1,若将y=kx+b向下平移,使平移后的直线与y轴交于F点,与双曲线交于D,E两点,若S△ABD=3,
求D,E的坐标.
(3)如图2,P为直线y=2上的一个动点,过点P作PQ∥y轴交直线AB于Q,交双曲线于R,若QR=2QP,求P点坐标.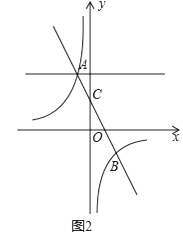
-
科目: 来源: 题型:
查看答案和解析>>【题目】因为
 ,所以
,所以 .这说明
.这说明 能被
能被 整除,同时也说明多项式
整除,同时也说明多项式 有一个因式为
有一个因式为 ;另外,当
;另外,当 多项式
多项式 的值为
的值为 .阅读上述材料回答问题:
.阅读上述材料回答问题:(1)由
 可知,当
可知,当 _时,多项式
_时,多项式 的值为
的值为 ;
;(2)一般地,如果一个关于字母
 的多项式
的多项式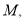 当
当 时,
时, 的值为
的值为 ,那么
,那么 与代数式
与代数式 之间有一定的关系,这种关系是:_____;
之间有一定的关系,这种关系是:_____;(3)已知关于
 的多项式
的多项式 能被
能被 整除,试求
整除,试求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小明家和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的是哪些地方?
(2)学校、商场和停车场分别在小明家的什么方位?
(3)如果学校距离小明家400m,那么商场和停车场分别距离小明家多远?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).
(1)补全坐标系并指出△ABC和△A'B'C'满足什么几何变换(直接写答案)?
(2)作△A'B'C'关于x轴对称图形△A''B''C'';
(3)△ABC和△A''B''C''满足什么几何变换?求A''、B''、C''三点坐标(直接写答案).

相关试题

