【题目】已知一次函数y=kx+b与反比例函数y= ![]() 交于A(﹣1,2),B(2,n),与y轴交于C点.
交于A(﹣1,2),B(2,n),与y轴交于C点.
(1)求反比例函数和一次函数解析式;
(2)如图1,若将y=kx+b向下平移,使平移后的直线与y轴交于F点,与双曲线交于D,E两点,若S△ABD=3,
求D,E的坐标.
(3)如图2,P为直线y=2上的一个动点,过点P作PQ∥y轴交直线AB于Q,交双曲线于R,若QR=2QP,求P点坐标.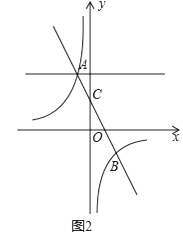
参考答案:
【答案】
(1)解:点A(﹣1,2)在反比例函数y= ![]() 的图象上,
的图象上,
∴m=(﹣1)×2=﹣2,
∴反比例函数的表达式为y=﹣ ![]() ,
,
∵点B(2,n)也在反比例函数的y=﹣ ![]() 图象上,
图象上,
∴n=﹣1,
即B(2,﹣1)
把点A(﹣1,2),点B(2,﹣1)代入一次函数y=kx+b中,得 ![]() ,
,
解得:k=﹣1,b=1,
∴一次函数的表达式为y=﹣x+1,
答:反比例函数的表达式是y=﹣ ![]() ,一次函数的表达式是y=﹣x+1;
,一次函数的表达式是y=﹣x+1;
(2)解:如图1,
连接AF,BF,
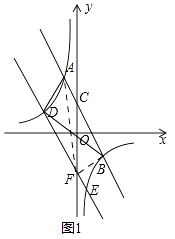
∵DE∥AB,
∴S△ABF=S△ABD=3(同底等高的两三角形面积相等),
∵直线AB的解析式为y=﹣x+1,
∴C(0,1),
设点F(0,m),
∴AF=1﹣m,
∴S△ABF=S△ACF+S△BCF= ![]() CF×|xA|+
CF×|xA|+ ![]() CF×|xB|=
CF×|xB|= ![]() (1﹣m)×(1+2)=3,
(1﹣m)×(1+2)=3,
∴m=﹣1,
∴F(0,﹣1),
∵直线DE的解析式为y=﹣x+1,且DE∥AB,
∴直线DE的解析式为y=﹣x﹣1①.
∵反比例函数的表达式为y=﹣ ![]() ②,
②,
联立①②解得, ![]() 或
或 ![]()
∴D(﹣2,1),E(1,﹣2);
(3)解:如图2
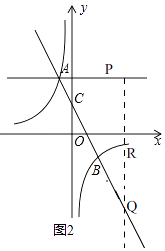
由(1)知,直线AB的解析式为y=﹣x﹣1,双曲线的解析式为y=﹣ ![]() ,
,
设点P(p,2),
∴Q(p,﹣p﹣1),R(p,﹣ ![]() ),
),
PQ=|2+p+1|,QR=|﹣p﹣1+ ![]() |,
|,
∵QR=2QP,
∴|﹣p﹣1+ ![]() |=2|2+p+1|,
|=2|2+p+1|,
解得,p= ![]() 或p=
或p= ![]() ,
,
∴P( ![]() ,2)或(
,2)或( ![]() ,2)或(
,2)或( ![]() ,2)或(
,2)或( ![]() ,2).
,2).
【解析】(1)把A的坐标代入反比例函数的解析式可求得m的值,从而可得到反比例函数的解析式;把点A和点B的坐标代入一次函数的解析式可求得一次函数的解析式;
(2)依据同底等高的两个三角形的面积相等可得到S△ABF=S△ABD=3,再利用三角形的面积公式可求得点F的坐标,即可得出直线DE的解析式,即可求出交点坐标;
(3)设点P(p,2),则Q(p,﹣p﹣1),R(p,﹣ ![]() ),然后可表示出PQ与QR的长度,最后依据QR=2QP,可得到关于p的方程,从而可求得p的值,从而可得到点P的坐标.
),然后可表示出PQ与QR的长度,最后依据QR=2QP,可得到关于p的方程,从而可求得p的值,从而可得到点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③
 (∠α+∠β);④
(∠α+∠β);④ (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分; B:49-45分;C:44-40分;D:39-30分;E:29-0分).每段包含最高分,不包含最低分,统计表如下,统计图如图所示.
分数段
频数(人)
百分比
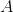













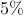

根据上面提供的信息,回答下列问题:
(1)在统计表中,
 的值为___,
的值为___,  的值为__,并将统计图补充完整.
的值为__,并将统计图补充完整.(2)成绩在40分以上定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知I是△ABC的内心,AI延长线交△ABC外接圆于D,连BD.

(1)在图1中,求证:DB=DI;
(2)如图2,若AB为直径,且OI⊥AD于I点,DE切圆于D点,求sin∠ADE的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)如图1,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE交于F,连DE,求证:DFDA=DBDC;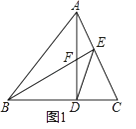
(2)如图2,若∠BAC=90°,AD⊥BC于D,F为线段AD上一点,在AD延长线上找一点G使AD2=DFDG,请画出图形找出点G并加以证明;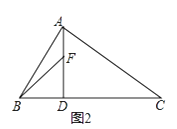
(3)如图3,在(1)的条件下,若∠ABC=45°,EF=1,EC=3,直接写出BD长.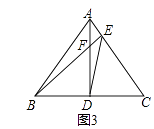
-
科目: 来源: 题型:
查看答案和解析>>【题目】因为
 ,所以
,所以 .这说明
.这说明 能被
能被 整除,同时也说明多项式
整除,同时也说明多项式 有一个因式为
有一个因式为 ;另外,当
;另外,当 多项式
多项式 的值为
的值为 .阅读上述材料回答问题:
.阅读上述材料回答问题:(1)由
 可知,当
可知,当 _时,多项式
_时,多项式 的值为
的值为 ;
;(2)一般地,如果一个关于字母
 的多项式
的多项式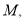 当
当 时,
时, 的值为
的值为 ,那么
,那么 与代数式
与代数式 之间有一定的关系,这种关系是:_____;
之间有一定的关系,这种关系是:_____;(3)已知关于
 的多项式
的多项式 能被
能被 整除,试求
整除,试求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小明家和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的是哪些地方?
(2)学校、商场和停车场分别在小明家的什么方位?
(3)如果学校距离小明家400m,那么商场和停车场分别距离小明家多远?

相关试题

