【题目】如图,FE⊥AB于点E,AC⊥BF于点C,连结AF,EC,点M,N分别为AF,EC的中点,连结ME,MC. 
(1)求证:ME=MC.
(2)连结MN,若MN=8,EC=12,求AF的长.
参考答案:
【答案】
(1)证明:∵FE⊥AB,
∴∠AEF=90°,
∵M为AF中点,
∴EM= ![]() AF,
AF,
∵AC⊥BF,
∴∠ACF=90°,
∴CM= ![]() AF,
AF,
∴EM=CM
(2)解:∵N为EC中点,EM=CM,
∴MN⊥EC,CN= ![]() EC,
EC,
∵EC=12,
∴CN=6,
∵MN=8,
∴MC= ![]() =10,
=10,
∴AF=20.
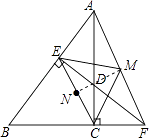
【解析】(1)首先根据FE⊥AB于点E,AC⊥BF于点C可得△AEF和△ACF是直角三角形,再根据在直角三角形中,斜边上的中线等于斜边的一半可得结论;(2)首先连接MN,根据等腰三角形的性质可得MN⊥EC,再利用勾股定理计算出MC的长,然后再计算AF长即可.
【考点精析】本题主要考查了直角三角形斜边上的中线的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组式子中,是同类项的是( )
A.3x2y与﹣3xy2
B.3xy与﹣2yx
C.2x与2x2
D.5xy与5yz -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x-9的平方根是±3,x+y的立方根是3.
(1)求x,y的值;
(2)x-y的平方根是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市今年九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分组(A:30分;B:29﹣27分;C:26﹣24分;D:23﹣18分;E:17﹣0分)统计如下:

根据上面提供的信息,回答下列问题:
(1)这次调查中,抽取的学生人数为多少?并将条形统计图补充完整;
(2)如果把成绩在24分以上(含24分)定为优秀,估计该市今年6000名九年级学生中,体育成绩为优秀的学生人数有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,抛物线
 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,直线l经过点A和点C,连接BC.将直线l沿着x轴正方形平移m个单位
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,直线l经过点A和点C,连接BC.将直线l沿着x轴正方形平移m个单位 得到直线
得到直线 ,
,  交
交 轴于点D,交BC于点E,交抛物线于点F.
轴于点D,交BC于点E,交抛物线于点F.(1)求点
 ,点
,点 和点
和点 的坐标
的坐标(2)如图2,将
 沿直线
沿直线 翻折得到
翻折得到 ,求点
,求点 的坐标(用含
的坐标(用含 的代数式表示);
的代数式表示);(3)在(2)的条件下,当点
 落在直线
落在直线 上时,请直接写出点
上时,请直接写出点 的坐标
的坐标
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣22×7﹣(﹣3)×6+5;
(2)( ﹣
﹣  ﹣
﹣ 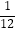 )×24÷(﹣2);
)×24÷(﹣2);
(3)56×1 +56×(﹣
+56×(﹣  )﹣56×
)﹣56×  ;
;
(4)(﹣1)4﹣ ×[2﹣(﹣3)2].
×[2﹣(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB第一次能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
相关试题

