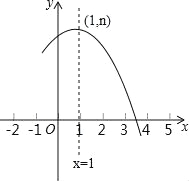
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
参考答案:
【答案】C
【解析】
试题分析:∵抛物线与x轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣2,0)和(﹣1,0)之间.∴当x=﹣1时,y>0,即a﹣b+c>0,所以①正确;∵抛物线的对称轴为直线x=﹣![]() =1,即b=﹣2a,∴3a+b=3a﹣2a=a,所以②错误;∵抛物线的顶点坐标为(1,n),∴
=1,即b=﹣2a,∴3a+b=3a﹣2a=a,所以②错误;∵抛物线的顶点坐标为(1,n),∴![]() =n,∴b2=4ac﹣4an=4a(c﹣n),所以③正确;∵抛物线与直线y=n有一个公共点,∴抛物线与直线y=n﹣1有2个公共点,∴一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④正确.故选C.
=n,∴b2=4ac﹣4an=4a(c﹣n),所以③正确;∵抛物线与直线y=n有一个公共点,∴抛物线与直线y=n﹣1有2个公共点,∴一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根,所以④正确.故选C.
-
科目: 来源: 题型:
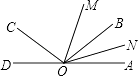
查看答案和解析>>【题目】如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
-
科目: 来源: 题型:
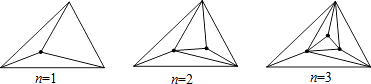
查看答案和解析>>【题目】一个三角形内有n个点,在这些点及三角形顶点之间用线段连接起来,使得这些线段互不相交,且又能把原三角形分割为不重叠的小三角形.如图:若三角形内有1个点时此时有3个小三角形;若三角形内有2个点时,此时有5个小三角形.则当三角形内有3个点时,此时有个小三角形;当三角形内有n个点时,此时有个小三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB、CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点随之停止运动.(设运动时间为t秒)
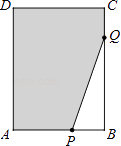
(1)如果存在某一时刻恰好使QB=2PB,求出此时t的值;
(2)在(1)的条件下,求图中阴影部分的面积(结果保留整数). -
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法对1.895取近似数,1.895≈______.(精确到0.01)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果数轴上的点A对应的数为-1,那么数轴上与点A相距3个单位长度的点所对应的有理数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师打算购买装扮学校“六一”儿童节活动会场,气球种类有笑脸和爱心两种.两种气球的价格不同,但同一种类的气球价格相同.由于会场布置需要,购买了的三束气球(每束4个气球),每束价格如图所示.

(1)若笑脸气球的单价是x元,请用含x的代数式表示第②束、第③束气球的总价格;(要求化简后,填在图形中)
(2)若第②束气球的总价钱比第③束气球的总价钱少2元,求这两种类的气球的单价.
相关试题

