【题目】如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB、CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点随之停止运动.(设运动时间为t秒) 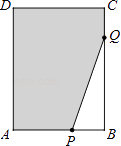
(1)如果存在某一时刻恰好使QB=2PB,求出此时t的值;
(2)在(1)的条件下,求图中阴影部分的面积(结果保留整数).
参考答案:
【答案】
(1)解:由题意可知AP=2t,CQ=t,
∴PB=AB﹣AP=6﹣2t,QB=CB﹣CQ=8﹣t.
当QB=2PB时,有8﹣t=2(6﹣2t).
解这个方程,得 ![]() .
.
所以当 ![]() 秒时,QB=2PB
秒时,QB=2PB
(2)解:当 ![]() 时,
时, ![]() ,
,
![]() .
.
∴ ![]() .
.
∵S长方形ABCD=ABCB=6×8=48,
∴S阴影=S长方形ABCD﹣S△QPB≈37
【解析】(1)当t秒QB=2PB时,BP=6﹣2t,BQ=8﹣t,就有8﹣t=2(6﹣2t),求出结论就可以了;(2)由(1)求出t的值就可以求出BP、BQ的值,根据矩形的面积减去三角形BPQ的面积就可以求出结论.
【考点精析】利用两点间的距离和三角形的面积对题目进行判断即可得到答案,需要熟知同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记;三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知4y2+my+1是完全平方式,则常数m的值是_________
-
科目: 来源: 题型:
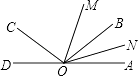
查看答案和解析>>【题目】如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
-
科目: 来源: 题型:
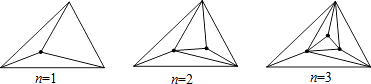
查看答案和解析>>【题目】一个三角形内有n个点,在这些点及三角形顶点之间用线段连接起来,使得这些线段互不相交,且又能把原三角形分割为不重叠的小三角形.如图:若三角形内有1个点时此时有3个小三角形;若三角形内有2个点时,此时有5个小三角形.则当三角形内有3个点时,此时有个小三角形;当三角形内有n个点时,此时有个小三角形.
-
科目: 来源: 题型:
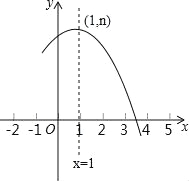
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法对1.895取近似数,1.895≈______.(精确到0.01)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果数轴上的点A对应的数为-1,那么数轴上与点A相距3个单位长度的点所对应的有理数为 .
相关试题

