【题目】如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且∠BFE=∠C.
(1)求证: ![]() ;
;
(2)若AB=4,∠BAE=30°,求AE的长.

参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)可通过证明∠BAF=∠AED,∠AFB=∠D,证得△ABF∽△EAD;
(2)先证出∠ABE=90°,再运用三角函数即可求出AE.
试题解析:(1)∵四边形ABCD是平行四边形
∴AD//BC,
∴∠C+∠ADE=180°
∵BFE=∠C,

∴∠AFB=∠EDA
又∵AB//DC
∴∠BAE=∠AED
∴![]() .
.
(2)∵AB//CD,BE⊥CD,
∴∠ABE=90°,
又∵AB=4,∠BAE=30°
设AE=x,则![]()
由勾股定理得![]()
解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=400m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:
 ,
, )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】快递员开摩托车从总部A点出发,在一条南北公路上来回收取包裹,现在记录下他连续行驶的情况(以向南为正方向,单位:千米):5,2,-4,
 ,3,-2.5,6.请问
,3,-2.5,6.请问(1)他最后一次收取包裹后在出发点A的什么位置?
(2)如果摩托车每千米耗油30毫升,出发前摩托车有油1000毫升,快递员在收完包裹后能回到总部吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两车分别从A. B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶。

(1)A、B两地的距离___千米;乙车速度是___;a=___.
(2)乙出发多长时间后两车相距330千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,∠C=900,BC=
 AB,BD平分∠ABC,BD=2,则以下结论错误的是 ( )
AB,BD平分∠ABC,BD=2,则以下结论错误的是 ( )
A. 点D在AB的垂直平分线上 B. 点D到AB的距离为1
C. 点A到BD的距离为2 D. 点B到AC的距离为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
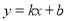 的图象经过
的图象经过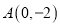 、
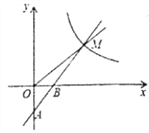
、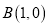 两点,与反比例函数的图象在第一象限内交于点M,△OBM的面积为2.
两点,与反比例函数的图象在第一象限内交于点M,△OBM的面积为2.(1)求一次函数和反比例函数的表达式;
(2)求AM的长度;
(3)P是x轴上一点,当AM⊥PM时,求出点P的坐标.
相关试题

