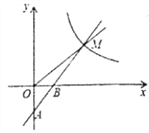
【题目】如图,一次函数![]() 的图象经过
的图象经过![]() 、
、![]() 两点,与反比例函数的图象在第一象限内交于点M,△OBM的面积为2.
两点,与反比例函数的图象在第一象限内交于点M,△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)求AM的长度;
(3)P是x轴上一点,当AM⊥PM时,求出点P的坐标.
参考答案:
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)(11,0)
;(3)(11,0)
【解析】试题分析: (1)根据一次函数y=k1x+b的图像经过A、B可得b、k1的方程组,进而求得一次函数的解析式,设M(m,n)作MD⊥x轴于点D,由△OBM的面积为2可求出n的值,将M(m,4)代入y=2x-2求出m的值,由M点在双曲线上求出k2,进而得到反比例函数的解析式;
(2)根据已知构造直角三角形进而利用勾股定理求出AM的长;
(3)过点M作MP⊥AM交x轴于点P,由MD⊥BP求出∠PMD=∠MBD=∠ABO,再由锐角三角形函数的定义求出OP的值,进而可得出结论.
试题解析:(1)∵直线![]() 的图象经过
的图象经过![]() 、
、![]() 两点
两点
∴![]() ,
,
∴解得: ![]()
∴一次函数的表达式为![]() ,
,
∴设![]() ,作MD⊥x轴于点D
,作MD⊥x轴于点D
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴n=4,
∴将![]() 代入
代入![]() 得
得![]() ,
,
∴m=3
∵![]() 在双曲线
在双曲线![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴反比例函数的表达式为: ![]() ;
;
则FM=3,AF=4+2=6,
∴![]() ;
;
(3)过点![]() 作MP⊥AM交x轴于点P,
作MP⊥AM交x轴于点P,
∵MD⊥BP,
∴∠PMD=∠MBD=∠ABO
∴![]() ,
,
∴在Rt△PDM中, ![]() ,
,
∴PD=2MD=8,
∴OP=OD+PD=11
∴当PM⊥AM,此时点P的坐标为(11,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且∠BFE=∠C.
(1)求证:
 ;
;(2)若AB=4,∠BAE=30°,求AE的长.

-
科目: 来源: 题型:
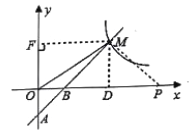
查看答案和解析>>【题目】甲乙两车分别从A. B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶。

(1)A、B两地的距离___千米;乙车速度是___;a=___.
(2)乙出发多长时间后两车相距330千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,∠C=900,BC=
 AB,BD平分∠ABC,BD=2,则以下结论错误的是 ( )
AB,BD平分∠ABC,BD=2,则以下结论错误的是 ( )
A. 点D在AB的垂直平分线上 B. 点D到AB的距离为1
C. 点A到BD的距离为2 D. 点B到AC的距离为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD相交于点O,如果
 ABC的周长比
ABC的周长比 AOB的周长长10厘米,则矩形边AD的长是
AOB的周长长10厘米,则矩形边AD的长是
A. 5厘米B. 10厘米
C. 7.5厘米D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理;
(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,求△ACE为等腰三角形时CE:CD的值;
(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.
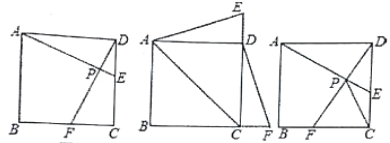
图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( )
 A、2
A、2B、4
C、
D、
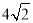
相关试题

