【题目】不等式组  的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解: 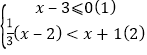
由①得,x≤3;
由②得,x>﹣ ![]() ;所以,不等式组的解集为﹣
;所以,不等式组的解集为﹣ ![]() <x≤3.
<x≤3.
故选A.
【考点精析】解答此题的关键在于理解不等式的解集在数轴上的表示的相关知识,掌握不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈,以及对一元一次不等式组的解法的理解,了解解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题引入:

(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=(用α表示);如图②,∠CBO= ∠ABC,∠BCO=
∠ABC,∠BCO=  ∠ACB,∠A=α,则∠BOC=(用α表示)拓展研究:
∠ACB,∠A=α,则∠BOC=(用α表示)拓展研究:
(2)如图③,∠CBO= ∠DBC,∠BCO=
∠DBC,∠BCO=  ∠ECB,∠A=α,请猜想∠BOC=(用α表示),并说明理由.
∠ECB,∠A=α,请猜想∠BOC=(用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO= ∠DBC,∠BCO=
∠DBC,∠BCO=  ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= . -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.

(1)若苗圃园的面积为72平方米,求x;
(2)若平行与墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y=x2﹣3x+m,直线l:y=kx(k>0),当k=1时,抛物线C与直线l只有一个公共点.

(1)求m的值;
(2)若直线l与抛物线C交于不同的两点A,B,直线l与直线l1:y=﹣3x+b交于点P,且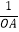 +
+  =
=  ,求b的值;
,求b的值;
(3)在(2)的条件下,设直线l1与y轴交于点Q,问:是否在实数k使S△APQ=S△BPQ?若存在,求k的值,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中不正确的是( )
A.函数y=2x的图象经过原点
B.函数y= 的图象位于第一、三象限
的图象位于第一、三象限
C.函数y=3x﹣1的图象不经过第二象限
D.函数y=﹣ 的值随x的值的增大而增大
的值随x的值的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为
( )
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0
②4a+2b+c>0
③4ac﹣b2<8a
④ <a<
<a< 
⑤b>c.
其中含所有正确结论的选项是( )
A.①③
B.①③④
C.②④⑤
D.①③④⑤
相关试题

