【题目】某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,60千米/时=
≈1.73,60千米/时= ![]() 米/秒)
米/秒) 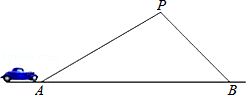
参考答案:
【答案】解:过点P作PC⊥AB于点C. 在Rt△APC中,tan∠PAC= ![]() ,
,
∴AC= ![]() =50
=50 ![]() ≈86.5(米),
≈86.5(米),
同理,BC= ![]() =PC=50(米),
=PC=50(米),
∴AB=AC+BC≈136.5(米),
60千米/时= ![]() 米/秒,
米/秒,
则136.5÷ ![]() ≈8.2>8.1.
≈8.2>8.1.
故这辆车通过AB段超速.
【解析】过点P作PC⊥AB于点C,在Rt△APC中,tan∠PAC= ![]() ,代入数据可得AC的长,同理可得BC的长,然后再求和即可得到AB的长,再利用路程初一速度可得时间,再与8.1秒进行比较,可得答案.
,代入数据可得AC的长,同理可得BC的长,然后再求和即可得到AB的长,再利用路程初一速度可得时间,再与8.1秒进行比较,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架5米长的梯子AB斜靠在一面墙上,梯子底端B到墙底的垂直距离BC为3米.
(1)求这个梯子的顶端A到地面的距离AC的值;
(2)如果梯子的顶端A沿墙AC竖直下滑1米到点D处,求梯子的底端B在水平方向滑动了多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=6,AB=10,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:

组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
请结合图表完成下列各题:
(1)①表中a的值为;②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是 .
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=kx+b交x轴于点A,交y轴于点B,直线y=2x﹣4交x轴于点D,与直线AB相交于点C(3,2).
(1)根据图象,写出关于x的不等式2x﹣4>x+b的解集;
(2)若点A的坐标为(5,0),求直线AB的解析式;
(3)在(2)的条件下,求四边形BODC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)求证:DE=AF;
(2)若AB=4,BG=3,求AF的长;
(3)如图2,连接DF、CE,判断线段DF与CE的位置关系并证明.
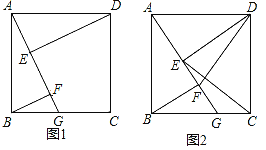
相关试题

