【题目】一次函数![]() 的图像
的图像![]() 随
随![]() 增大而减小,且经过点
增大而减小,且经过点![]() .
.
求(1)![]() 的值;
的值;
(2)求该直线与坐标轴围成的三角形的面积及坐标原点到直线的距离.
参考答案:
【答案】(1)![]() ;(2)该直线与坐标轴围成的三角形的面积为
;(2)该直线与坐标轴围成的三角形的面积为![]() ,坐标原点到直线的距离为
,坐标原点到直线的距离为![]() .
.
【解析】
(1)由一次函数的定义和性质列出方程和不等式求出m的值,代入A点坐标,可求出n值;
(2)由解析式可得![]() 轴截距与
轴截距与![]() 轴截距,然后根据三角形面积公式求解;利用勾股定理求出直线与坐标轴围成的三角形的斜边长,然后用等积法求解.
轴截距,然后根据三角形面积公式求解;利用勾股定理求出直线与坐标轴围成的三角形的斜边长,然后用等积法求解.
解:(1)![]()
![]() 是一次函数
是一次函数
![]()
![]()
即![]()
解得![]() ;
;![]() .
.
又![]()
![]() 随
随![]() 增大而减小
增大而减小
![]()
![]()
即![]()
![]()
![]()
![]() 一次函数解析式为:
一次函数解析式为:![]()
代入点![]() 得
得![]()
![]() n=9
n=9
![]()
![]()
(2)由(1)得:![]()
![]() 轴截距:
轴截距:![]()
![]() 轴截距:
轴截距:![]()
![]() 该直线与坐标轴围成的三角形的面积:
该直线与坐标轴围成的三角形的面积:![]()
该直线与坐标轴围成的三角形的斜边长:![]()
设坐标原点到直线的距离为![]() .
.
有![]()
![]()
![]()
![]() 坐标原点到直线的距离为
坐标原点到直线的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”
(1)请直接写出两个为“同簇二次函数”的函数:①______,②_________;
(2)已知关于
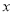 的二次函数
的二次函数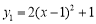 和
和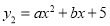 ,若
,若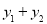 与
与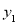 为“同簇二次函数”,求函数
为“同簇二次函数”,求函数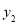 的表达式,并求出当
的表达式,并求出当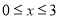 时,
时,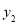 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
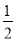 x﹣2与x轴交于点A,以OA为斜边在x轴上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=
x﹣2与x轴交于点A,以OA为斜边在x轴上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=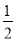 x﹣2上时,则△OAB平移的距离是_____.
x﹣2上时,则△OAB平移的距离是_____.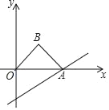
-
科目: 来源: 题型:
查看答案和解析>>【题目】在创建文明城区的活动中,有两端长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度
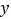 (米)与施工时间
(米)与施工时间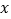 (时)之间的关系的部分图像.请解答下列问题.
(时)之间的关系的部分图像.请解答下列问题.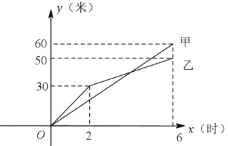
(1)甲队在
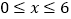 的时段内的速度是 米/时.乙队在
的时段内的速度是 米/时.乙队在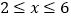 的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米,乙队铺设彩色道砖的长度是 米.
的时段内的速度是 米/时. 6小时甲队铺设彩色道砖的长度是 米,乙队铺设彩色道砖的长度是 米.(2)如果铺设的彩色道砖的总长度为150米,开挖6小时后,甲队、乙队均增加人手,提高了工作效率,此后乙队平均每小时比甲队多铺5米,结果乙反而比甲队提前1小时完成总铺设任务.求提高工作效率后甲队、乙队每小时铺设的长度分别为多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 图像与y轴、x轴分别交于A、B两点
图像与y轴、x轴分别交于A、B两点(1)求点A、B坐标和∠BAO度数
(2)点C、D分别是线段OA、AB上一动点(不与端点重合),且CD=DA,设线段OC的长度为x ,
 ,请求出y关于x的函数关系式以及定义域
,请求出y关于x的函数关系式以及定义域(3)点C、D分别是射线OA、射线BA上一动点,且CD=DA,当ΔODB为等腰三角形时,求C的坐标(第(3)小题直接写出分类情况和答案,不用过程)


相关试题

