【题目】本学期实验中学组织开展课外兴趣活动,各活动小班根据实际情况确定了计划组班人数,并发动学生自愿报名,报名人数与计划人数的前5位情况如下.若用同一小班的报名人数与计划人数的比值大小来衡量进入该班的难易程度,则由表中数据,可预测( )
小班名称 | 奥数 | 写作 | 舞蹈 | 篮球 | 航模 |
报名人数 | 215 | 201 | 154 | 76 | 65 |
小班名称 | 奥数 | 舞蹈 | 写作 | 合唱 | 书法 |
计划人数 | 120 | 100 | 90 | 80 | 70 |
A.奥数比书法容易
B.合唱比篮球容易
C.写作比舞蹈容易
D.航模比书法容易
参考答案:
【答案】B
【解析】解答:由题意得:同一小班的报名人数与计划人数的比值越小进入该班的难度大, ∵表中数据为报名人数与计划人数的前5位的统计情况,
∴篮球、航模计划人数不多于70;合唱、书法报名人数不多于65,
同一小班的报名人数与计划人数的比值为:奥数 ![]() =1.79;写作
=1.79;写作 ![]() =2.23;舞蹈
=2.23;舞蹈 ![]() =1.54;篮球>
=1.54;篮球> ![]() =1.09;航模<1;合唱<1;书法<1;
=1.09;航模<1;合唱<1;书法<1;
∵1.79>1,∴书法比奥数困难,因此A错误;
∵1<1.09,∴篮球比合唱容易,因此B正确;
∵2.23>1.54,∴舞蹈比写作困难,因此C错误;
∵航模与书法比值相近,无法判断,因此D错误.
故选:B.
分析:处理此类问题,首先读懂统计表,认清其结构,求得每个班中报名人数与计划人数的比值,比值越小则越难.由此进行解答.此题考查从统计表中获取信息的能力.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
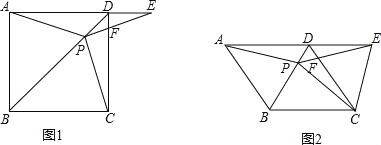
(1)求∠CPE的度数;
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师对某班全体学生在电脑培训前后进行了一次水平测试,考分以同一标准划分为“不合格”、“合格”、“优秀”三个等级,成绩见下表.下列说法错误的是( )
成绩
培训前
培训后
不合格
40
10
合格
8
25
优秀
2
15
A.培训前“不合格”的学生占80%
B.培训前成绩“合格”的学生是“优秀”学生的4倍
C.培训后80%的学生成绩达到了“合格”以上
D.培训后优秀率提高了30% -
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:已知|a﹣2|+(b+1)2=0,求﹣(3a2﹣4ab)+[b2﹣2(2a2+2ab)]的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果+3吨表示运入仓库的大米吨数, 那么运出5吨大米表示为( )
A.-3吨 B.+3吨 C.-5吨 D.+5吨
-
科目: 来源: 题型:
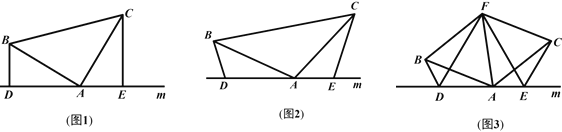
查看答案和解析>>【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点
互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
相关试题

