【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
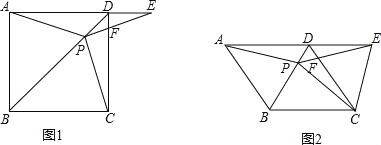
(1)求∠CPE的度数;
(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
参考答案:
【答案】(1)90°;(2)AP=CE.理由参见解析.
【解析】
试题分析:(1)先证出△ABP≌△CBP,根据全等三角形的性质得到∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PE,得到∠DAP=∠E,于是∠DCP=∠E,又因为∠PFC=∠DFE,所以∠CPF=∠EDF=90°,从而得到结论;(2)根据菱形的性质得到AB=BC,∠ABP=∠CBP=60°,根据全等三角形的性质得到PA=PC,∠BAP=∠BCP,根据等量减等量差相等和等腰三角形的性质得到∠DAP=∠DCP,∠DAP=∠AEP,等量代换得到∠DCP=∠AEP,∠EPC=∠EDC=60°,PE=PC=PA,推出△EPC是等边三角形,即可得到结论.
试题解析:(1)先证出△ABP≌△CBP,在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,在△ABP和△CBP中,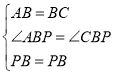 ,∴△ABP≌△CBP(SAS),∴PA=PC,∠BAP=∠BCP,∴∠DAP=∠DCP,∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E,∵∠CFP=∠EFD(对顶角相等),∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,即∠CPF=∠EDF=90°;(2)根据题意,在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,在△ABP和△CBP中,
,∴△ABP≌△CBP(SAS),∴PA=PC,∠BAP=∠BCP,∴∠DAP=∠DCP,∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E,∵∠CFP=∠EFD(对顶角相等),∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,即∠CPF=∠EDF=90°;(2)根据题意,在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,在△ABP和△CBP中, ,∴△ABP≌△CBP(SAS),∴PA=PC,∠BAP=∠BCP,∴∠DAP=∠DCP,又∵PA=PE,∴PC=PE,∵PA=PE,∴∠DAP=∠AEP,∴∠DCP=∠AEP,∵∠CFP=∠EFD(对顶角相等),∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,∴△EPC是等边三角形,∴PC=CE,∴AP=CE.
,∴△ABP≌△CBP(SAS),∴PA=PC,∠BAP=∠BCP,∴∠DAP=∠DCP,又∵PA=PE,∴PC=PE,∵PA=PE,∴∠DAP=∠AEP,∴∠DCP=∠AEP,∵∠CFP=∠EFD(对顶角相等),∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,∴△EPC是等边三角形,∴PC=CE,∴AP=CE.
-
科目: 来源: 题型:
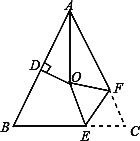
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=kx+b经过第一、二、四象限,则k,b的取值范围是( )
A. k>0, b>0 B. k>0,b<0 C. k<0,b>0 D. k<0,b<0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=5x2﹣mx+n,B=﹣3y2+2x﹣1,若A+B中不含有一次项和常数项,则代数式m2﹣2mn+n2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师对某班全体学生在电脑培训前后进行了一次水平测试,考分以同一标准划分为“不合格”、“合格”、“优秀”三个等级,成绩见下表.下列说法错误的是( )
成绩
培训前
培训后
不合格
40
10
合格
8
25
优秀
2
15
A.培训前“不合格”的学生占80%
B.培训前成绩“合格”的学生是“优秀”学生的4倍
C.培训后80%的学生成绩达到了“合格”以上
D.培训后优秀率提高了30% -
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:已知|a﹣2|+(b+1)2=0,求﹣(3a2﹣4ab)+[b2﹣2(2a2+2ab)]的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期实验中学组织开展课外兴趣活动,各活动小班根据实际情况确定了计划组班人数,并发动学生自愿报名,报名人数与计划人数的前5位情况如下.若用同一小班的报名人数与计划人数的比值大小来衡量进入该班的难易程度,则由表中数据,可预测( )
小班名称
奥数
写作
舞蹈
篮球
航模
报名人数
215
201
154
76
65
小班名称
奥数
舞蹈
写作
合唱
书法
计划人数
120
100
90
80
70
A.奥数比书法容易
B.合唱比篮球容易
C.写作比舞蹈容易
D.航模比书法容易
相关试题

