【题目】已知:如图,在平面直角坐标系xOy中,直线![]() 与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA﹣QO|的取值范围.

参考答案:
【答案】(1)C(3,0),![]() ;(2)直线BC上不存在符合条件的点P;(3)0≤|QA﹣QO|≤4.
;(2)直线BC上不存在符合条件的点P;(3)0≤|QA﹣QO|≤4.
【解析】
试题分析:(1)点A的坐标是纵坐标为0,得横坐标为8,所以点A的坐标为(8,0);
点B的坐标是横坐标为0,解得纵坐标为6,所以点B的坐标为(0,6);
由题意得:BC是∠ABO的角平分线,所以OC=CH,BH=OB=6.∵AB=10,∴AH=4,设OC=x,则AC=8﹣x,由勾股定理得:x=3,∴点C的坐标为(3,0),将此三点代入二次函数一般式,列的方程组即可求得;
(2)求得直线BC的解析式,根据平行四边形的性质,对角相等,对边平行且相等,借助于三角函数即可求得;
(3)如图,由对称性可知QO=QH,|QA﹣QO|=|QA﹣QH|.
当点Q与点B重合时,Q、H、A三点共线,|QA﹣QO|取得最大值4(即为AH的长);
设线段OA的垂直平分线与直线BC的交点为K,当点Q与点K重合时,|QA﹣QO|取得最小值0.
试题解析:(1)点C的坐标为(3,0).∵点A、B的坐标分别为A(8,0),B(0,6),∴可设过A、B、C三点的抛物线的解析式为y=a(x﹣3)(x﹣8).
将x=0,y=6代入抛物线的解析式,得![]() ,∴过A、B、C三点的抛物线的解析式为
,∴过A、B、C三点的抛物线的解析式为![]() .
.
(2)可得抛物线的对称轴为直线![]() ,顶点D的坐标为(
,顶点D的坐标为(![]() ,
,![]() ),设抛物线的对称轴与x轴的交点为G.∵直线BC的解析式为y=﹣2x+6.
),设抛物线的对称轴与x轴的交点为G.∵直线BC的解析式为y=﹣2x+6.
设点P的坐标为(x,﹣2x+6).
解法一:如图,作OP∥AD交直线BC于点P,连接AP,作PM⊥x轴于点M.
∵OP∥AD,∴∠POM=∠GAD,tan∠POM=tan∠GAD,∴![]() ,即
,即 .
.
解得![]() .
.
经检验![]() 是原方程的解.
是原方程的解.
此时点P的坐标为(![]() ,
,![]() ).
).
但此时OM=![]() ,GA=
,GA=![]() ,OM<GA.
,OM<GA.
∵OP=![]() ,AD=
,AD=![]() ,∠POM=∠GAD,∴OP<AD,即四边形的对边OP与AD平行但不相等,∴直线BC上不存在符合条件的点P.
,∠POM=∠GAD,∴OP<AD,即四边形的对边OP与AD平行但不相等,∴直线BC上不存在符合条件的点P.

解法二:如图,取OA的中点E,作点D关于点E的对称点P,作PN⊥x轴于点N.则∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG.
由OE=![]() OA=4,可得E点的坐标为(4,0).
OA=4,可得E点的坐标为(4,0).
NE=EG=![]() ,ON=OE﹣NE=
,ON=OE﹣NE=![]() ,NP=DG=
,NP=DG=![]() ,∴点P的坐标为(
,∴点P的坐标为(![]() ,
,![]() ).
).
∵x=![]() 时,-2x+6=
时,-2x+6=![]() =1≠
=1≠![]() ,∴点P不在直线BC上,∴直线BC上不存在符合条件的点P.
,∴点P不在直线BC上,∴直线BC上不存在符合条件的点P.

(3)|QA﹣QO|的取值范围是0≤|QA﹣QO|≤4.
当Q在OA的垂直平分线上与直线BC的交点时,(如点K处),此时OK=AK,则|QA﹣QO|=0,当Q在AH的延长线与直线BC交点时,此时|QA﹣QO|最大,直线AH的解析式为:![]() ,直线BC的解析式为:y=﹣2x+6,联立可得:交点为(0,6),∴OQ=6,AQ=10,∴|QA﹣QO|=4,∴|QA﹣QO|的取值范围是:0≤|QA﹣QO|≤4.
,直线BC的解析式为:y=﹣2x+6,联立可得:交点为(0,6),∴OQ=6,AQ=10,∴|QA﹣QO|=4,∴|QA﹣QO|的取值范围是:0≤|QA﹣QO|≤4.

-
科目: 来源: 题型:
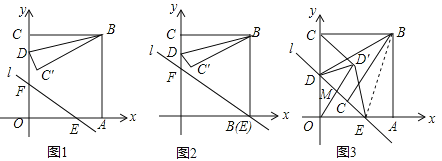
查看答案和解析>>【题目】如图1,在直角坐标系xoy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.
(1)当∠CBD=15°时,求点C′的坐标.
(2)当图1中的直线l经过点A,且
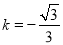 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.(3)当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点O为原点,点A的坐标为(﹣6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.
(1)如图2,若α=60°,OE=OA,求直线EF的函数表达式;
(2)若α为锐角,tanα=
 ,当AE取得最小值时,求正方形OEFG的面积;
,当AE取得最小值时,求正方形OEFG的面积;(3)当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为
 :1?若能,求点P的坐标;若不能,试说明理由.
:1?若能,求点P的坐标;若不能,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从3开始,连续的3的倍数相加,它们和的情况如表:
加数的个数n
和S
1
3=1×3
2
3+6=9=3×3
3
3+6+9=18=6×3
4
3+6+9+12=30=10×3
5
3+6+9+12+15=45=15×3
根据以上规律,可知当n=10时,S的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AO⊥BC,DO⊥OE.

(1)在下面的横线上填上适当的角:
∠DOE=∠+∠;∠BOE=∠﹣∠;
(2)不添加其它条件情况下,请尽可能多地写出图中有关角的等量关系(至少4个).
(3)如果∠COE=35°,求∠AOD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
(1)当OC∥AB时,∠BOC的度数为 ;
(2)连接AC,BC,在点C在⊙O运动过程中,△ABC的面积是否存在最大值?并求出△ABC的最大值;
(3)直接写出在(2)的条件下D点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意解答
(1)化简:(﹣x3)2+(2x2)3+(x﹣3)﹣2
(2)计算: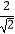 ﹣
﹣ 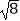 +(
+( 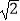 ﹣1)0 .
﹣1)0 .
相关试题

