【题目】我国![]() 道路交通安全法
道路交通安全法![]() 第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”
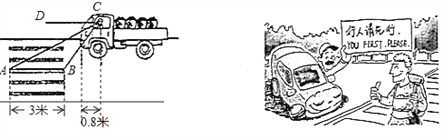
第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行” ![]() 如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是
如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是![]() 和
和![]() ,如果斑马线的宽度是
,如果斑马线的宽度是![]() 米,驾驶员与车头的距离是
米,驾驶员与车头的距离是![]() 米,这时汽车车头与斑马线的距离x是多少?
米,这时汽车车头与斑马线的距离x是多少?
参考答案:
【答案】0.7米
【解析】试题分析:直接利用已知得出∠BAC=∠BCA,则BC=AB,再得出BF的长,求出x的值即可.
试题解析:
解:如图所示:延长AB,
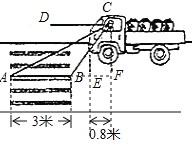
∵CD∥AB,
∴∠CAB=30°,∠CBF=60°,
∴∠BCA=60°-30°=30°,即∠BAC=∠BCA,
∴BC=AB=3m,
在Rt△BCF中,BC=3m,∠CBF=60°,
∴BF=![]() BC=1.5m,
BC=1.5m,
故x=BF-EF=1.5-0.8=0.7(m),
答:这时汽车车头与斑马线的距离x是0.7m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.(1)由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图
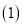 所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则
所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则 ______
______(2)如图(2),是由若干个完全相同的小正方体组成的一个几何体
①请画出这个几何体的左视图和俯视图;
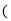 用阴影表示
用阴影表示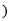
②如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加______个小正方体?
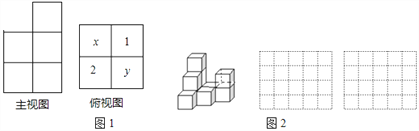
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方形ABCD中,AB=CD=8cm,AD=BC=6cm,点E是DC边上一点,且CE=1cm,动点P从A点出发,沿折线A-D-E以acm/s的速度向终点E运动,运动时间为t秒,已知a是方程
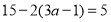 的解.
的解.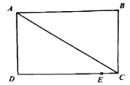
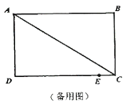
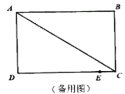
(1)求a的值;
(2)点P在运动过程中,请用t的式子表示△APC的面积;
(3)在点P运动的同时,有一动点Q从C点出发,沿折线C-D-A以1cm/s的速度向终点A运动,运动过程中,一个点停止运动时另一个点继续向终点运动,当△APC和△AQC的面积相差6平方厘米时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,BC=6,P为AD上一动点,把△ABP沿BP翻折,使点A落在点F处,连接CF,若BF=CF,则AP的长为_____.
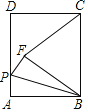
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组乘一辆检修车沿一段东西方向铁路检修,规定向东走为正,向西走为负,小组的出发地记为M,某天检修完毕时,行走记录(单位:千米)如下:
+12,-5,-9,+10,-4,+15,-9,+3,-6,-3,-7
(1)问收工时,检修小组距出发地M有多远?在东侧还是西侧?
(2)若检修车每千米耗油0.2升,求从出发到收工时检修车共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填在相应的集合里:
-2.4,3,
 ,
, ,0.333…,-(2.28),3.14,
,0.333…,-(2.28),3.14, ,1.010010001…(相邻两个1之间0的个数增加1),
,1.010010001…(相邻两个1之间0的个数增加1), .
.(1)正有理数集合{ ……}
(2)整数集合{ ……}
(3)负分数集合{ ……}
(4)无理数集合{ ……}
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年4月23日,是第25个世界读书日.为了解学生每周阅读时间,某校随机抽取了部分学生进行调查,根据调查结果,将阅读时间x(单位:小时)分成了4组,A:0≤x<2;B:2≤x<4;C:4≤x<6;D:6≤x<8,试结合图中所给信息解答下列问题:
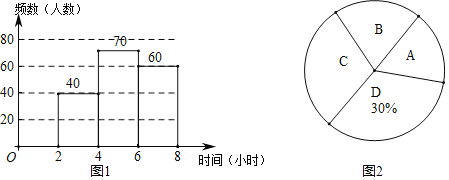
(1)这次随机抽取了 名学生进行调查;扇形统计图中,扇形B的圆心角的度数为 .
(2)补全频数分布直方图;
(3)若该校共有2000名学生,试估计每周阅读时间不少于4小时的学生共有多少名?
相关试题

