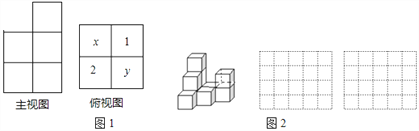
【题目】.(1)由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图![]() 所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则
所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则![]() ______
______
(2)如图(2),是由若干个完全相同的小正方体组成的一个几何体
①请画出这个几何体的左视图和俯视图; ![]() 用阴影表示
用阴影表示![]()
②如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加______个小正方体?
参考答案:
【答案】(1)4或5;(2) ①见解析;②4.
【解析】试题分析:(1)俯视图中的每个数字是该位置小立方体的个数,结合主视图2列中的个数,分析其中的数字,从而求解.
(2)①由已知条件可知,主视图有3列,每列小正方数形数目分别为3,1,2,左视图有3列,每列小正方形数目分别为3,2,1;俯视图有3列,每列小正方数形数目分别为3,2,1,据此可画出图形.
②根据题意结合左视图与俯视图不变得出答案.
试题解析:
解:(1)由俯视图可知,该组合体有两行两列,
左边一列前一行有两个正方体,结合主视图可知左边一列叠有2个正方体,故x=1或2;
由主视图右边一列可知,右边一列最高可以叠3个正方体,故y=3,
则x+y=4或x+y=5,
故答案为:4或5.
(2)①如图所示:
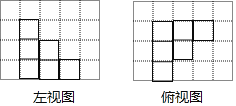
②可在最底层第二列第三行加一个,第三列第二行加2个,第三列第三行加1个,共4个.
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,E是CB延长线上一个动点,F、G分别为AE、BC的中点,FG与ED相交于点H.
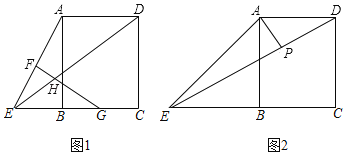
(1)求证:HE=HG;
(2)如图2,当BE=AB时,过点A作AP⊥DE于点P,连接BP,求PQ与PB的数量关系,并说明理由.
-
科目: 来源: 题型:
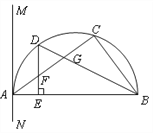
查看答案和解析>>【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线AB∥CD,将一块三角板EFG如图1所示,△EFG的边与直线AB、CD分别相交于M,N两点,∠F=90°,∠E=30°.
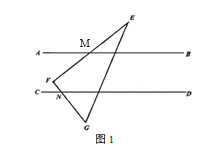
(1)求证:∠EMB+∠DNG=90°
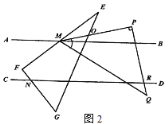
(2)将另一块三角板MPQ如图2放置,△MPQ的边PQ、PM分别与直线CD相交于点R,与△EFG的EG相交于点O,∠P=90°,∠PMQ=45°,直接写出∠PMB与∠PRD的数量关系:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方形ABCD中,AB=CD=8cm,AD=BC=6cm,点E是DC边上一点,且CE=1cm,动点P从A点出发,沿折线A-D-E以acm/s的速度向终点E运动,运动时间为t秒,已知a是方程
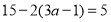 的解.
的解.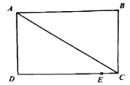
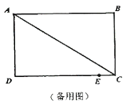
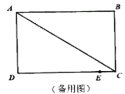
(1)求a的值;
(2)点P在运动过程中,请用t的式子表示△APC的面积;
(3)在点P运动的同时,有一动点Q从C点出发,沿折线C-D-A以1cm/s的速度向终点A运动,运动过程中,一个点停止运动时另一个点继续向终点运动,当△APC和△AQC的面积相差6平方厘米时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,BC=6,P为AD上一动点,把△ABP沿BP翻折,使点A落在点F处,连接CF,若BF=CF,则AP的长为_____.
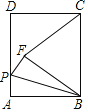
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国
 道路交通安全法
道路交通安全法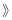 第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”
第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”  如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是
如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是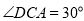 和
和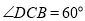 ,如果斑马线的宽度是
,如果斑马线的宽度是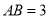 米,驾驶员与车头的距离是
米,驾驶员与车头的距离是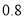 米,这时汽车车头与斑马线的距离x是多少?
米,这时汽车车头与斑马线的距离x是多少?
相关试题

