【题目】快、慢两车分别从相距480km路程的甲、乙两地同时出发，匀速行驶，先相向而行，途中慢车因故停留1h，然后以原速继续向甲地行驶，到达甲地后停止行驶；快车到达乙地后，立即按原路原速返回甲地（快车掉头的时间忽略不计），快、慢两车距乙地的路y km与所用时间x h之间的函数图象如图，请结合图象信息解答下列问题：
（1）直接写出慢车的行驶速度和a的值；
（2）求快车的速度和B点坐标；
（3）快车与慢车第一次相遇时，距离甲地的路程是多少千米？

参考答案：

【答案】
（1）解：由题意，得

慢车的速度为：480÷（9﹣1）=60千米/时，

∴a=60×（7﹣1）=360千米．

答：慢车的行驶速度为60千米/时，a的值为360千米


（2）解：由题意，得：5×60=300，

∴D（5，300），设yOD=k1x，由题意，得300=5k1，

∴k1=60，

∴yOD=60x．

∵快车的速度为：（480+360）÷7=120千米/时．

∴480÷120=4小时．

∴B（4，0），C（8，480）．


（3）解：设yAB=k2x+b，由题意，得：

，

解得： ，

∴yAB=﹣120x+480，

∴ ，

解得： ，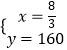

∴480﹣160=320千米．

答：快车与慢车第一次相遇时，距离甲地的路程是320千米


【解析】（1）根据行程问题的数量关系：速度=路程÷时间及路程=速度×时间就可以得出结论；（2）由（1）的结论可以求出点D的坐标，再由题意可以求出快车的速度就可以求出点B的坐标．（3）由待定系数法求出AB的解析式及OD的解析式就可以求出结论．

关闭