【题目】如图,在平面直角坐标系中,□ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=![]() (x<0)与y=
(x<0)与y=![]() (x>0)的图象上,则□ABCD的面积为____.
(x>0)的图象上,则□ABCD的面积为____.

参考答案:
【答案】5
【解析】连接OA、OD,如图,利用平行四边形的性质得AD垂直y轴,则利用反比例函数的比例系数k的几何意义得到S△OAE=![]() ,S△ODE=
,S△ODE=![]() ,所以S△OAD=2,然后根据平行四边形的面积公式可得到□ABCD的面积=2S△OAD=4.
,所以S△OAD=2,然后根据平行四边形的面积公式可得到□ABCD的面积=2S△OAD=4.
解:连接OA、OD,如图,
∵四边形ABCD为平行四边形,
∴AD垂直y轴,
∴S△OAE=![]() ×|﹣3|=
×|﹣3|=![]() ,S△ODE=
,S△ODE=![]() ×|1|=
×|1|=![]() ,
,
∴S△OAD=2,
∴ABCD的面积=2S△OAD=4.
故答案为4.

“点睛”此题考查了反比例函数的k的几何意义及平行四边形的性质,根据题意得出◇ABCD的面积等于矩形ADOE的面积是解答本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2xa+1-3yb-2=10是一个二元一次方程,则a-b=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形ABC的面积为1cm2 . AP垂直∠B的平分线BP于点P.则三角形PBC的面积是
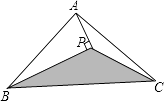
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
A. 上午8时 B. 上午9时30分 C. 上午10时 D. 上午12时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下: 如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
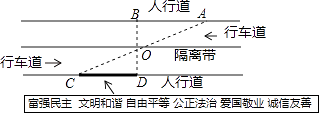
相关试题

