【题目】如图,已知二次函数y=ax2+ ![]() x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC.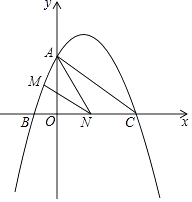
(1)请直接写出二次函数y=ax2+ ![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时N的坐标.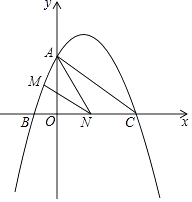
参考答案:
【答案】
(1)
解:将点A和点C的坐标代入得: ![]() ,
,
解得:a=﹣ ![]() ,c=4.
,c=4.
∴该二次函数的解析式为y=﹣ ![]() x2+
x2+ ![]() x+4
x+4
(2)
解:令y=0得:﹣ ![]() x2+
x2+ ![]() x+4=0,解得:x=﹣2或x=8,
x+4=0,解得:x=﹣2或x=8,
∴点B(﹣2,0).
∴BC=10.
在Rt△AOB和Rt△AOC中,依据勾股定理可知:AB2=OB2+AO2=20,AC2=OA2+OC2=80,
∴AB2+AC2=BC2.
∴△ABC为直角三角形
(3)
解:设点N的坐标为(n,0)(﹣2<n<8),则BN=n+2,CN=8﹣n.
∵MN∥AC,
∴ ![]() =
= ![]() .
.
∵AO=4,BC=10,
∴S△ABC= ![]() BCAO=
BCAO= ![]() ×4×10=20.
×4×10=20.
∴S△ABN= ![]() S△ABC=2(n+2).
S△ABC=2(n+2).
∴S△AMN= ![]() S△AMN=
S△AMN= ![]() (8﹣n)(n+2)=﹣
(8﹣n)(n+2)=﹣ ![]() (n﹣3)2+5.
(n﹣3)2+5.
∴当n=3时,即N(3,0)时,△AMN的面积最大,最大值为5
【解析】(1)将点A和点C的坐标代入代入抛物线的解析式,求得a,c的值即可;(2)先求得点B的坐标,从而得到BC=10,然后依据勾股定理可求得AB2、AC2的值,最后依据勾股定理的逆定理进行判断即可;(3)设点N的坐标为(n,0)(﹣2<n<8),则BN=n+2,CN=8﹣n,利用平行线分线段成比例定理可得到 ![]() =
= ![]() ,然后依据等高的两个三角形的面积比等于底边的长度比可得到S△AMN与n的函数关系式,最后利用二次函数的性质可求得△AMN的面积取得最大值时点N的坐标.
,然后依据等高的两个三角形的面积比等于底边的长度比可得到S△AMN与n的函数关系式,最后利用二次函数的性质可求得△AMN的面积取得最大值时点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线AB与x、y轴分别交于点A(4,0)、B(0,
 )两点,∠BAO的角平分线交y轴于点D,点C为直线AB上一点以AC为直径的⊙G经过点D,且与x轴交于另一点E.
)两点,∠BAO的角平分线交y轴于点D,点C为直线AB上一点以AC为直径的⊙G经过点D,且与x轴交于另一点E. 
(1)求证:y轴是⊙G的切线.
(2)求出⊙G的半径;
(3)连结EC,求△ACE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD、
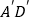 分别是锐角三角形ABC和锐角三角形
分别是锐角三角形ABC和锐角三角形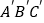 中BC、
中BC、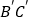 边上的高,且
边上的高,且 、
、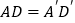 .若使△ABC≌△
.若使△ABC≌△ ,请你补充条件_________.(填写一个你认为适当的条件即可)
,请你补充条件_________.(填写一个你认为适当的条件即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=4∠DOE,∠COE=
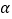 ,则∠BOE的度数为( )
,则∠BOE的度数为( )
A. 360°-4
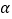 B. 180°-4
B. 180°-4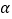 C.
C. 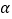 D. 270°-3
D. 270°-3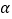
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。
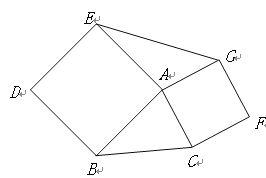
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ∶∠BOC=( )

A. 1∶2 B. 1∶3 C. 2∶5 D. 1∶4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图22,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB的平分线上.
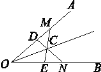
相关试题

