【题目】如图,在直角坐标系中,直线AB与x、y轴分别交于点A(4,0)、B(0, ![]() )两点,∠BAO的角平分线交y轴于点D,点C为直线AB上一点以AC为直径的⊙G经过点D,且与x轴交于另一点E.
)两点,∠BAO的角平分线交y轴于点D,点C为直线AB上一点以AC为直径的⊙G经过点D,且与x轴交于另一点E. 
(1)求证:y轴是⊙G的切线.
(2)求出⊙G的半径;
(3)连结EC,求△ACE的面积.
参考答案:
【答案】
(1)解:连接GD,如图1,

∵∠OAB的角平分线交y轴于点D,
∴∠GAD=∠DAO,
∵GD=GA,
∴∠GDA=∠GAD,
∴∠GDA=∠DAO,
∴GD∥OA,
∴∠BDG=∠BOA=90°,
∵GD为半径,
∴y轴是⊙G的切线
(2)解:∵A(4,0),B(0, ![]() ),
),
∴OA=4,OB= ![]() ,
,
在Rt△AOB中,由勾股定理可得:AB= ![]() ,
,
设半径GD=r,则BG= ![]() ﹣r,
﹣r,
∵GD∥OA,
∴△BDG∽△BOA,
∴ ![]() ,
,
![]() r=4(
r=4( ![]() ﹣r),
﹣r),
∴r=2.5
(3)解:连接CE,如图2,

∵AC是圆的直径,
∴∠AEC=∠BOE=90°,
∴CE∥OB,
∴△ACE∽△ABO,
∴ ![]() ,
,
设OE=a,则AE=4﹣a,
∴CE= ![]() (4﹣a),
(4﹣a),
∵CE2+AE2=AC2,
∴ ![]() (4﹣a)2+(4﹣a)2=25,
(4﹣a)2+(4﹣a)2=25,
∴a=1或a=7(不合题意,舍去)
∴AE=3,由勾股定理可得CE=4,
∴△ACE的面积= ![]() AECE=
AECE= ![]() ×3×4=6.
×3×4=6.
【解析】(1)连接DG,要证明y轴是⊙G的切线,只需要连接GD后证明GD⊥OB即可.(2)由(1)可知GD∥OA,则△BDG∽△BOA,设半径为r后,利用对应边的比相等列方程即可求出半径r的值.(3)连接CE,设OE=a,则AE=4﹣a,易证△ACE∽△ABO,由相似三角形的性质可得到CE和OE数量关系,再利用勾股定理可求出a的值,进而可求出数△ACE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A∶∠B∶∠C=3∶5∶10,又△MNC≌△ABC,则∠BCM∶∠BCN等于( )

A. 1∶2 B. 1∶3 C. 2∶3 D. 1∶4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,
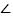 AOD=120
AOD=120 ,
, 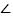 AOC=90
AOC=90 ,OE平分
,OE平分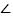 BOD,则图中彼此互补的角共有( )
BOD,则图中彼此互补的角共有( )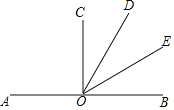
A. 4对 B. 5对 C. 6对 D. 7对
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为丰富学生的校园生活,准备从某体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.
(1)购买一个足球,一个篮球各需多少元?
(2)根据学校的实际情况,需从该体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD、
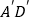 分别是锐角三角形ABC和锐角三角形
分别是锐角三角形ABC和锐角三角形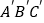 中BC、
中BC、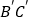 边上的高,且
边上的高,且 、
、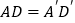 .若使△ABC≌△
.若使△ABC≌△ ,请你补充条件_________.(填写一个你认为适当的条件即可)
,请你补充条件_________.(填写一个你认为适当的条件即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=4∠DOE,∠COE=
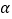 ,则∠BOE的度数为( )
,则∠BOE的度数为( )
A. 360°-4
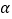 B. 180°-4
B. 180°-4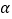 C.
C. 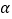 D. 270°-3
D. 270°-3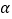
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+
 x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC.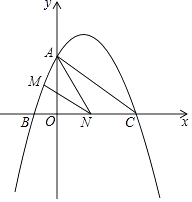
(1)请直接写出二次函数y=ax2+ x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时N的坐标.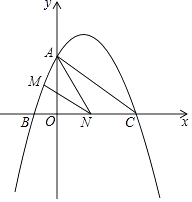
相关试题

