【题目】OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ∶∠BOC=( )

A. 1∶2 B. 1∶3 C. 2∶5 D. 1∶4
参考答案:
【答案】D
【解析】
依据OM是∠AOB平分线,OQ是∠MOA平分线,可得∠AOQ=![]() ∠AOM=
∠AOM=![]() ∠AOB,依据ON是∠AOC平分线,OP是∠NOA平分线,可得∠AOP=
∠AOB,依据ON是∠AOC平分线,OP是∠NOA平分线,可得∠AOP=![]() ∠AON=
∠AON=![]() ∠AOC=
∠AOC=![]() (∠AOB+∠BOC),进而得出∠POQ:∠BOC=1:4.
(∠AOB+∠BOC),进而得出∠POQ:∠BOC=1:4.
解:∵OM是∠AOB平分线,OQ是∠MOA平分线,

∴∠AOQ=![]() ∠AOM=
∠AOM=![]() ∠AOB,
∠AOB,
∵ON是∠AOC平分线,OP是∠NOA平分线,
∴∠AOP=![]() ∠AON=
∠AON=![]() ∠AOC=
∠AOC=![]() (∠AOB+∠BOC),
(∠AOB+∠BOC),
∴∠POQ=∠AOP-∠AOQ
=![]() (∠AOB+∠BOC)-
(∠AOB+∠BOC)-![]() ∠AOB,
∠AOB,
=![]() ∠BOC,
∠BOC,
∴∠POQ:∠BOC=1:4,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=4∠DOE,∠COE=
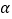 ,则∠BOE的度数为( )
,则∠BOE的度数为( )
A. 360°-4
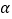 B. 180°-4
B. 180°-4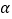 C.
C. 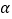 D. 270°-3
D. 270°-3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+
 x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B,C,点C的坐标为(8,0),连接AC.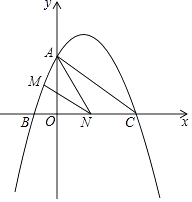
(1)请直接写出二次函数y=ax2+ x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时N的坐标.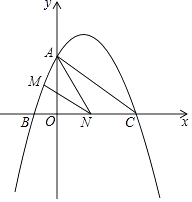
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。
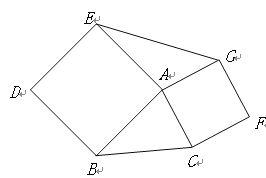
(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图22,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB的平分线上.
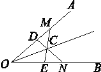
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出五个等量关系:①AD=BC ②AC=BD ③CE=DE ④∠D=∠C ⑤∠DAB=∠CBA.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】直线a∥b,直角三角形如图放置,若∠1+∠A=65°,则∠2的度数为( )

A.15°
B.20°
C.25°
D.30°
相关试题

