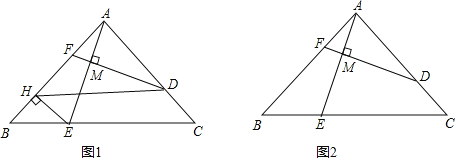
【题目】已知在Rt△ABC中,∠BAC=90°,AB≥AC,D,E分别为AC,BC边上的点(不包括端点),且![]() =
=![]() =m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
=m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
(1)如图1,过点E作EH⊥AB于点H,连结DH.
①求证:四边形DHEC是平行四边形;
②若m=![]() ,求证:AE=DF;
,求证:AE=DF;
(2)如图2,若m=![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)①证明见解析;②证明见解析;(2)![]()
【解析】(1)①先判断出△BHE∽△BAC,进而判断出HE=DC,即可得出结论;
②先判断出AC=AB,BH=HE,再判断出∠HEA=∠AFD,即可得出结论;
(2)先判断出△EGB∽△CAB,进而求出CD:BE=3:5,再判断出∠AFM=∠AEG进而判断出△FAD∽△EGA,即可得出结论.
(1)①证明:∵EH⊥AB,∠BAC=90°,
∴EH∥CA,
∴△BHE∽△BAC,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴HE=DC,
∵EH∥DC,
∴四边形DHEC是平行四边形;
②∵![]() ,∠BAC=90°,
,∠BAC=90°,
∴AC=AB,
∵![]() ,HE=DC,
,HE=DC,
∴HE=DC,
∴![]() ,
,
∵∠BHE=90°,
∴BH=HE,
∵HE=DC,
∴BH=CD,
∴AH=AD,
∵DM⊥AE,EH⊥AB,
∴∠EHA=∠AMF=90°,
∴∠HAE+∠HEA=∠HAE+∠AFM=90°,
∴∠HEA=∠AFD,
∵∠EHA=∠FAD=90°,
∴△HEA≌△AFD,
∴AE=DF;
(2)如图,过点E作EG⊥AB于G,
∵CA⊥AB,
∴EG∥CA,
∴△EGB∽△CAB,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴EG=CD,
设EG=CD=3x,AC=3y,
∴BE=5x,BC=5y,
∴BG=4x,AB=4y,
∵∠EGA=∠AMF=90°,
∴∠GEA+∠EAG=∠EAG+∠AFM,
∴∠AFM=∠AEG,
∵∠FAD=∠EGA=90°,
∴△FAD∽△EGA,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电力维修小组从
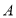 点出发,在东西线路上检修电线,如果规定向东为正,向西为负,一天中行驶里程(单位:千米)记录如下:+5,-4,-7,+8,-9,+6,+5
点出发,在东西线路上检修电线,如果规定向东为正,向西为负,一天中行驶里程(单位:千米)记录如下:+5,-4,-7,+8,-9,+6,+5(1)求收工时在
 地的什么方位?
地的什么方位?(2)在记录中,距离
 最远有 千米?
最远有 千米?(3)若每千米耗油0.2升,油价为5元/升,问出发到收工时共需要多少元油钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节约用水,某市决定调整居民用水收费方法,规定如果每户每月用水不超过10吨,每吨水收费2元,如果每户每月用水超过10吨,则超过部分每吨水收费2.5元;小红看到这种收费方法后,想算算她家每月的水费:
(1)如果小红家每月用水8吨,则水费是 元;如果小红家每月用水20吨,则水费是 元.
(2)如果字母
 表示小红家每月用水的吨数,那么小红家每月的水费该如何用
表示小红家每月用水的吨数,那么小红家每月的水费该如何用 的代数式表示呢?
的代数式表示呢? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF.
(1)试说明:△ABC≌△DFE;
(2)若BF=13,EC=7,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,如果在正方形中画
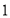 条纵线和
条纵线和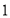 条横线,便把正方形分成
条横线,便把正方形分成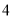 部分(如图①);如果在正方形中画
部分(如图①);如果在正方形中画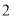 条纵线和
条纵线和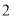 条横线,便把正方形分成
条横线,便把正方形分成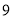 部分(如图②);如果在正方形中画
部分(如图②);如果在正方形中画 条纵线和
条纵线和 条横线,便把正方形分成
条横线,便把正方形分成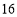 部分(如图③...如果在正方形中画
部分(如图③...如果在正方形中画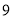 条纵线和
条纵线和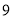 条横线.便把正方形分成( )部分
条横线.便把正方形分成( )部分
A.
 B.
B.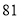 C.
C.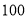 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正两位数的个位数字是a,十位数字比个位数字大2.
(1)列式表示这个两位数;
(2)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新数与原数的和能被22整除.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送
 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位: ):
):第
 批
批第
 批
批第
 批
批第
 批
批第
 批
批




(1)接送完第
 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?(2)若该出租车每千米耗油
 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?(3)若该出租车的计价标准为:行驶路程不超过
 收费
收费 元,超过
元,超过 的部分按每千米
的部分按每千米 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?
相关试题

