搜索
【题目】为了节约用水，某市决定调整居民用水收费方法，规定如果每户每月用水不超过10吨，每吨水收费2元，如果每户每月用水超过10吨，则超过部分每吨水收费2.5元；小红看到这种收费方法后，想算算她家每月的水费：
（1）如果小红家每月用水8吨，则水费是 元；如果小红家每月用水20吨，则水费是 元．
（2）如果字母
表示小红家每月用水的吨数，那么小红家每月的水费该如何用
的代数式表示呢？
参考答案：
【答案】（1）16、45；（2）x≤10时，2x元，x>10时，(2.5x-5)元
【解析】试题分析：每月用水
吨时，水费为： 
元；超过
吨，超过部分每吨水收费2
元，于是可得：每月用水
吨时，水费为： 
元.
分类讨论：①如果每月用水
吨，水费为： 
(元)，②如果每月用水
吨，水费为： 
(元).
试题解析：(1)每月用水
吨时，水费为： 
元，
每月用水
吨时,水费为： 
元；
(2)①如果每月用水
吨,水费为： 
(元)，
②如果每月用水
吨,水费为： 
(元).
故答案为：(1)16，45.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面的材料：
如图1，在数轴上A点衰示的数为a，B点表示的数为b，则点A到点B的距离记为AB．线段AB的长可以用右边的数减去左边的数表示，即AB﹣b﹣a．
请用上面的知识解答下面的问题：
如图2，一个点从数轴上的原点开始，先向左移动1cm到达A点，再向左移动2cm到达B点，然后向右移动7cm到达C点，用1个单位长度表示1cm．
（1）请你在数轴上表示出A．B．C三点的位置：
（2）点C到点人的距离CA= cm；若数轴上有一点D，且AD=4，则点D表示的数为 ；
（3）若将点A向右移动xcm，则移动后的点表示的数为 ；（用代数式表示）
（4）若点B以每秒2cm的速度向左移动，同时A．C点分别以每秒1cm、4cm的速度向右移动．设移动时间为t秒，
试探索：CA﹣AB的值是否会随着t的变化而改变？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各组数中：①﹣22与22；②（﹣3）2与32；③|﹣2|与﹣|﹣2|；④（﹣3）3与﹣33；⑤﹣3与﹣（+3），其中相等的共有（ ）
A. 4对 B. 3对 C. 2对 D. 1对
-
科目： 来源： 题型：
查看答案和解析>>【题目】某超市一月份的营业额为300万元，已知三月份的营业额为363万元，如果平均每月的增长率为x，由题意列方程________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点N是△ABC的边BC延长线上的一点，∠ACN=2∠BAC，过点A作AC的垂线交CN于点P．
（1）若∠APC=30°，求证：AB=AP；
（2）若AP=8，BP=16，求AC的长；
（3）若点P在BC的延长线上运动，∠APB的平分线交AB于点M．你认为∠AMP的大小是否发生变化？若变化，请说明理由；若不变化，求出∠AMP的大小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】旋转的性质:
（1）对应点到旋转中心的距离;
（2）任意一组对应点与旋转中心的连线所成的角等于;
（3）旋转前、后的图形. -
科目： 来源： 题型：
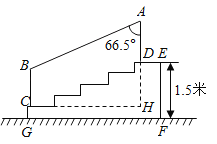
查看答案和解析>>【题目】如图，某城市市民广场一入口处有五级高度相等的小台阶．已知台阶总高1.5米，为了安全现要作一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC（杆子的地段分别为D、C），且∠DAB=66.5°．（参考数据：cos66.5°≈0.40，sin66.5°≈0.92）
（1）求点D与点C的高度DH；
（2）求所有不锈钢材料的总长度（即AD+AB+BC的长，结果精确到0.1米）
相关试题
