【题目】在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DF⊥BC,交AB的延长线于E,垂足为F.
(1)如图①,求证直线DE是⊙O的切线; 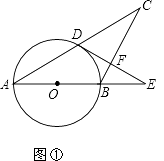
(2)如图②,作DG⊥AB于H,交⊙O于G,若AB=5,AC=8,求DG的长. 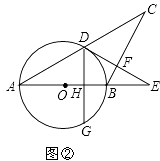
参考答案:
【答案】
(1)证明:连接OD,如图,

∵AB=BC,
∴∠A=∠C.
∵OA=OD,
∴∠A=∠ADO.
∴∠C=∠ADO.
∴OD∥BC.
∵DF⊥BC,
∴∠ODE=90°.
∴直线DE是⊙O的切线;
(2)解:连接DB,
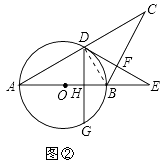
∵AB是⊙O的直径,
∴∠ADB=90°.
∵AB=BC,
∴AD=DC.
∵AC=8,
∴AD=4.
在Rt△ADB中,BD= ![]() =
= ![]() =3,
=3,
∵DG⊥AB于H,
由三角形面积公式,得ABDH=ADDB.
∴DH= ![]() =
= ![]() ,
,
∵AB⊥DG,
∴DG=2DH= ![]()
【解析】(Ⅰ)连接OD,由AB=BC,OA=OD,得到∠A=∠C,∠A=∠ADO,则∠C=∠ADO,得到OD∥BC;而DF⊥BC,则∠ODE=90°,根据切线的判定定理即可得到结论;(Ⅱ)连接BD,AB是⊙O的直径,根据圆周角定理的推论得到∠ADB=90°.而AB=BC,则AD=DC=4.在Rt△ADB中,利用勾股定理可计算出BD=3,再利用等积法得到ABDH=ADDB,可计算出DH,然后根据垂径定理得到DG=2DH.
【考点精析】关于本题考查的勾股定理的概念和圆周角定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.
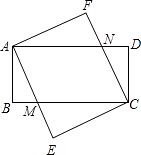
(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个公司为某敬老院各捐款300000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐款20元.则甲、乙两公司各有多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数﹣2表示的点重合,则数轴上数﹣4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:
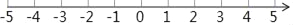
若数轴上数﹣3表示的点与数1表示的点重合.(根据此情境解决下列问题)
①则数轴上数3表示的点与数 表示的点重合.
②若点A到原点的距离是5个单位长度,并且A、B两点经折叠后重合,则B点表示的数是 .
③若数轴上M、N两点之间的距离为2018,并且M、N两点经折叠后重合,
如果M点表示的数比N点表示的数大,则M点表示的数是 .则N点表示的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABM=37°,AB=20,C是射线BM上一点.
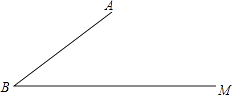
(1)求点A到BM的距离;
(2)在下列条件中,可以唯一确定BC长的是;(填写所有符合条件的序号)
①AC=13;②tan∠ACB= ;③连接AC,△ABC的面积为126.
;③连接AC,△ABC的面积为126.
(3)在(2)的答案中,选择一个作为条件,画出草图,求BC.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75) -
科目: 来源: 题型:
查看答案和解析>>【题目】先让我们一起来学习方程m2+1=
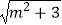 的解法:
的解法:
解:令m2=a,则a+1= ,方程两边平方可得,(a+1)2=a+3
,方程两边平方可得,(a+1)2=a+3
解得a1=1,a2=﹣2,∵m2≥0∴m2=1∴m=±1
点评:类似的方程可以用“整体换元”的思想解决.
不妨一试:
如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.
(1)求抛物线的解析式;
(2)①当P点运动到A点处时,通过计算发现:POPH(填“>”、“<”或“=”);
(3)当△PHO为等边三角形时,求点P坐标;
(4)如图2,设点C(1,﹣2),问是否存在点P,使得以P、O、H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.
相关试题

