【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )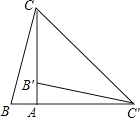
A.32°
B.64°
C.77°
D.87°
参考答案:
【答案】C
【解析】由旋转的性质可知,AC=AC′,
∵∠CAC′=90°,可知△CAC′为等腰直角三角形,则∠CC′A=45°.
∵∠CC′B′=32°,
∴∠C′B′A=∠C′CA+∠CC′B′=45°+32°=77°,
∵∠B=∠C′B′A ,
∴∠B=77°,
故选C.
旋转中心为点A , C、C′为对应点,可知AC=AC′,又因为∠CAC′=90°,根据三角形外角的性质求出∠C′B′A的度数,进而求出∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形的边长为2,建立合适的直角坐标系,写出各个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】①一个多边形的内角和等于它的外角和的3倍,则它是几边形?
②某学校想用地砖铺地,学校已准备了一批完全相同的正n边形[n为(1)中的所求值],如果单独用这种地砖能密铺吗?
③如果不能,请你自己只选用一种同(2)边长相同的正方形地砖搭配能密铺吗?如果能,请你画出一片密铺的示意图. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a、b是方程x2+x-2019=0的两个实数根,则a2+2a+b的值为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2x3﹣2k+2=4是关于x的一元一次方程,则k= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为 .
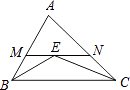
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 把它的解集表示在数轴上,并求出不等式组的非负整数解.
把它的解集表示在数轴上,并求出不等式组的非负整数解.
相关试题

